The identification of poplar clones by montecarlo methods: the random forests
Forest@ - Journal of Silviculture and Forest Ecology, Volume 2, Pages 217-224 (2005)
doi: https://doi.org/10.3832/efor0279-0020217
Published: Jun 08, 2005 - Copyright © 2005 SISEF
Research Articles
Guest Editors: RI.SELV.ITALIA - MiPAF Project
« Shared Research Program on Silviculture in Italy »
Collection/Special Issue: Massimo Bianchi
Abstract
Tests for distinctness, homogeneity and stability of Poplar clones are still based on the use of proper descriptors of the main morphological and phenetic characteristics of the plant. Although the importance of a precise identification of clones is widely acknowledged, no sound technique has yet come into wide use. Many descriptors related to economic and productivity traits show a reduced repeatability or within clone variability. A multivariate approach by means of parametric procedure is ineffective due to the joint presence of variables with different sampling properties. We have applied some new numerical techniques based on computer simulation approaches to overcome difficulties due to the probability distribution of different traits. Among others, the procedure known as Random Forest was particularly suitable for clones discrimination. Random Forest, proposed by Leo Breiman (University of California, Berkeley,USA), is based on the building of a large set (Forest) of classification trees, generated at random, which are allowed to evolve generation by generation on the basis of computer simulations. Some internal estimates are produced and they are useful to describe the classification process and the relative importance of single traits. In the evaluation of 30 poplar clones by means of 18 descriptors, we received a good classification performance with a mean misclassification rate of 0.13 and with 22 clones with a rate under this value. The procedure allowed individuating the best variables according to classification ability. Final aim of the work is to individuate simple rules that can be easily applied in the typical condition of nursery practice.
Keywords
Classification, Morphological traits, Populus, Random Forest
Introduzione
Le prove per l’identificazione, l’omogeneità e la stabilità di cloni di pioppo sono tuttora basate sull’uso di appropriati descrittori delle caratteristiche morfologiche della pianta ([6]). Anche se l’importanza di una sicura identificazione clonale è ampiamente riconosciuta, attualmente non vi sono tecniche soddisfacenti di uso generale. Molti descrittori legati a caratteristiche economiche o alla produttività presentano, infatti, scarsa ripetibilità ed elevata variabilità entro clone. Lo scarso potere discriminante di singoli caratteri può essere in parte ovviato ricorrendo ad un approccio multivariato. L’uso di caratteristiche morfologiche in funzione discriminante è stato affrontato da diversi autori ([4], [1]).
Dal punto di vista metodologico, si tratta di risolvere un problema di classificazione (supervised classification) in cui il numero di gruppi è noto, dato che corrisponde al numero dei cloni oggetto di studio. In primo luogo, si tratta di identificare il sottoinsieme di caratteri che riesce meglio ad attribuire una pianta incognita al proprio gruppo di appartenenza, cioè al clone (feature extraction). A tale scopo sono disponibili numerose tecniche tra le quali spiccano i metodi statistici perché offrono la possibilità di valutare l’incertezza riguardante sia la stima di eventuali parametri del modello che l’attribuzione di una pianta ad un certo clone.
Il criterio guida seguito in questo lavoro non è costituito dalla comprensione della struttura di covariazione dei caratteri considerati, e neppure dallo sviluppo di modelli parametrici sofisticati (e difficoltosi da gestire senza adeguato addestramento), ma consiste invece nella soluzione del problema di classificazione mediante regole semplici che possano essere facilmente applicate nella pratica vivaistica, al più ricorrendo a risorse di calcolo disponibili in un computer palmare.
Una promettente strategia recentemente sviluppata da Leo Breiman (University of California, Berkeley, USA) si basa sull’utilizzo di alberi di classificazione. L’autore ha esteso la tecnica degli alberi di classificazione integrandola in una procedura di simulazione Monte Carlo e la ha battezzata Random Forest: essa è basata sulla creazione di un insieme ampio (Forest) di alberi classificatori, ognuno dei quali si propone per classificare una singola pianta di cui sono stati valutati caratteri di qualsiasi natura. Confrontando le proposte di classificazione fornite da ogni albero della foresta emerge la classe (clone) a cui attribuire la pianta: essa è quella che ha ricevuto più indicazioni o voti.
Al fine di saggiare le potenzialità delle Foreste Casuali, abbiamo analizzato i dati sperimentali relativi a 30 cloni di pioppo, rappresentativi della collezione di germoplasma, ottenuti nell’ambito del Progetto Ri.Selv.Italia.
Complessivamente, abbiamo dimostrato che la procedura delle Foreste Casuali è particolarmente efficace per la discriminazione clonale. Tra gli aspetti più interessanti delle Foreste Casuali vi sono:
- la presenza di stime interne che permettono di descrivere il processo classificatorio e la sua efficienza;
- la capacità di gestire variabili classificatrici indipendenti di qualsiasi tipologia.
Il lavoro si apre con una prima sezione contenente le definizioni di albero di classificazione e di Random Forest. Viene poi introdotto il caso di studio, con i risultati dell’analisi di classificazione. Infine, sono discussi i risultati in relazione ad alcune problematiche aperte e le prospettive per sviluppi futuri del lavoro di classificazione.
Metodi numerici
Classificatori ad albero
Un classificatore è una regola che permette di attribuire una unità statistica ad un certo sottoinsieme sulla base del valore assunto da una o più variabili osservate o misurate sulla medesima unità statistica. In genere si indica con y la variabile che rappresenta il sottoinsieme (nel presente contesto indica il clone, y = 1, 2,..., 30) e con x = (x1, x2,...) il vettore riferito a tutte le variabili usate per la classificazione (ad esempio, la lunghezza del picciolo, il colore del fusto, eccetera). A titolo di esemplificazione una semplice regola potrebbe essere: “Se x1< 9 e x2 > 3 allora y = 3”, cioè tale unità statistica (pianta) è probabile appartenga al sottoinsieme (clone) 3.
Un albero di classificazione è una collezione di tali regole espresse in forma di albero binario, ottenute attraverso partizionamento ricorsivo ([2]). Tra i vantaggi derivati dall’uso di questa metodologia troviamo:
- facilità nell’interpretazione dei risultati quando si considerino contemporaneamente variabili qualitative e quantitative,
- l’invarianza rispetto a trasformazioni monotone delle variabili,
- adeguata trattazione dei valori mancanti,
- capacità di cogliere aspetti non lineari e interazioni di ordine elevato.
Formalmente, un classificatore h() associa ad ogni punto campionario x il corrispondente valore y*=h(x). Impiegando un insieme di risultati sperimentali D di in cui le osservazioni sono realizzazioni distribuite identicamente ed indipendentemente dalla distribuzione del vettore casuale (Y,X), e definita una funzione di perdita L[Y,h(X,D)] che quantifica la perdita dovuta alla discrepanza tra y* e y, si definisce errore di previsione il valore atteso PE(h,D) = EY,X [L(Y,h(X,D))].
Spesso la funzione di perdita vale uno oppure zero, cioè se per l’unità statistica u vale yu = yu* allora la perdita è nulla, ovvero osservato e previsto coincidono, altrimenti la perdita vale uno. L’insieme di dati D è comunemente detto training dataset. Ovviamente il classificatore migliore è quello che riduce al minimo l’errore di previsione.
Foreste stocastiche
Una Foresta Casuale (Random Forest, [3], modificato) è un classificatore costituito da una collezione di alberi di classificazione { h(x,T,Θk), k=1, 2,..., K } in cui {Θk } sono vettori identicamente ed indipendentemente distribuiti. Ogni albero della collezione (foresta) esprime un solo voto per attribuire ad una classe l’unità statistica sulla base del vettore di valori x: la scelta finale è di attribuire l’unità statistica alla classe per la quale si è ottenuta la maggioranza dei voti, cioè per la quale si è espressa la maggioranza degli alberi della foresta casuale.
La classificazione basata su foreste stocastiche ha caratteristiche statistiche molto interessanti:
- E’ relativamente robusta rispetto ad osservazioni estreme (outliers) ed al rumore sperimentale.
- E’ più veloce di molte altre procedure di classificazione numerica.
- Consente stime interne dell’errore, della correlazione e dell’importanza delle variabili utilizzate nel processo di classificazione.
- E’ relativamente semplice e può essere implementata su calcolatori paralleli in modo efficiente.
- E’ facilmente paralellelizzabile.
Uno dei punti fondamentali che caratterizzano le Foreste Casuali è che l’errore di generalizzazione converge “quasi certamente” per un numero di alberi della foresta che diverge ed è pertanto scongiurata l’eventualità di operare una sovrastrutturazione (overfitting) della procedura complessiva di classificazione a causa dell’aumento del numero di alberi.
Identificazione delle variabili rilevanti ai fini della classificazione (feature extraction)
Breiman ha proposto quattro misure le quali, in base alla struttura emersa nell’analisi dei risultati della simulazione Monte Carlo, quantificano la rilevanza di ogni variabile. Nella misura 1, l’importanza della m-esima variabile è valutata al k-esimo albero attraverso la permutazione di tutti i valori di tale variabile e valutando tale permutazione come una nuova covariata classificatoria. Ottenuta la classificazione ne deriva anche un nuovo valore di errore interno. La differenza tra errore prima della permutazione ed errore dopo la permutazione rappresenta l’importanza della variabile m-esima.
Nella misura 2 e nella misura 3, si considera, alla fine della simulazione, il margine dell’n-esima unità statistica. Il margine è dato dalla proporzione dei voti per la sua vera classe di appartenenza (nota) meno il massimo tra le proporzioni di voti per ognuna delle rimanenti classi. La seconda misura per la m-esima variabile si ottiene come media dei margini che si sono abbassati per ogni caso quando la variabile m-esima è permutata come per la misura 1. La misura 3 rappresenta il conteggio di quanti margini si sono abbassati diminuita del numero di margini che si sono alzati.
Nella misura 4, ad ogni suddivisione, una delle variabili è usata per formare la suddivisione, evento che comporta una riduzione dell’indice del Gini. La somma di tutti i decrementi nella foresta dovuti ad una certa variabile, normalizzato per il numero di alberi, costituisce la misura 4.
Software
L’applicazione delle procedure descritte è implementata tramite software gentilmente fornito da L. Breiman. Il numero di variabili di suddivisione per ogni albero è stato fissato a tre, come da suggerimento dell’Autore stesso.
Risultati
Nell’ambito di un progetto di ricerca volta allo sviluppo di modelli d’analisi congiunta di descrittori con differenti proprietà distributive, abbiamo analizzato i dati relativi a trenta cloni di pioppo (Tab. 1), iscritti a registro e rappresentativi della raccolta di germoplasma, e rilevati a cura dell’Istituto di sperimentazione per la Pioppicoltura di Casale Monferrato.
Tab. 1 - Elenco dei cloni inseriti nella valutazione, loro denominazione e specie di appartenenza.
| # | Denominazione | Specie | # | Denominazione | Specie |
|---|---|---|---|---|---|
| 1 | Jean Pourtet | P. nigra | 16 | Soligo | P. x canadensis |
| 2 | Vereecken | P. nigra | 17 | Taro | P. x canadensis x generosa |
| 3 | Carolina di Santena | P. x canadensis | 18 | Bellini | P. x canadensis |
| 4 | Dora | P. x canadensis | 19 | Brenta | P. x canadensis |
| 5 | Lambro | P. x canadensis | 20 | Cima | P. x canadensis |
| 6 | Lux | P. deltoides | 21 | Guardi | P. x canadensis |
| 7 | Oglio | P. deltoides | 22 | Luisa Avanzo | P. x canadensis |
| 8 | Dvina | P. deltoides | 23 | Neva | P. x canadensis |
| 9 | Onda | P. deltoides | 24 | Blanc de Poitou | P. x canadensis |
| 10 | San Martino | P. x canadensis | 25 | I-154 II | P. x canadensis |
| 11 | I-45/51 | P. x canadensis | 26 | I-214 | P. x canadensis |
| 12 | Stura | P. x canadensis | 27 | I-262 | P. x canadensis |
| 13 | Triplo | P. x canadensis | 28 | I-455 | P. x canadensis |
| 14 | Lena II | P. deltoides | 29 | I-476 | P. x canadensis |
| 15 | Sile | P. deltoides x ciliata | 30 | Panaro | P. x canadensis |
Il disegno sperimentale è strutturato in due località (Casale Monferrato e Mantova) con 10 repliche in ognuna. In ciascuna replica sono stati rilevati 18 descrittori, sia qualitativi che quantitativi, su due piante per ogni clone.
Le linee guida UPOV relative al pioppo elencano più di 50 descrittori, con le relative classi qualitative nelle quali la variabilità osservata viene codificata. Nel nostro caso abbiamo utilizzato 12 di questi, considerati maggiormente utili per la classificazione del materiale. Ad essi sono stati aggiunti sei caratteri quantitativi riferiti alla misurazione di alcune caratteristiche della foglia. Questi ultimi sono stati rilevati in laboratorio su campioni di foglie appartenenti alle stesse piante le cui caratteristiche sono state osservate in vivaio. I caratteri rilevati sono elencati in Tab. 2.
Tab. 2 - Caratteri valutati, loro caratteristica distributiva (D = discreta; C = continua) e nome codificato. FMS="foglie" maggiormente sviluppate.
| Carattere | D/C | Nome codificato | Carattere | D/C | Nome codificato |
|---|---|---|---|---|---|
| Sezione del fusto | D | sezione | Colore nervatura centrale | D | colorenc |
| Colore del fusto | D | colorefu | Num. ghiandole peziolari | D | numghia |
| Pelosità del germoglio | D | pelos | Ondulazione del margine | D | ondulama |
| Portamento foglie (FMS) in relazione al fusto | D | portamento | Profilo della superficie della lamina tra nervature | D | profilone |
| Colore germoglio apicale | D | colore | Lunghezza del picciolo (cm) | C | picciolo |
| Forma inserzione picciolo sulla lamina | D | inspic | Lunghezza nervatura centrale (NC) (cm) | C | nervcent |
| Forma della base della lamina delle FMS | D | formaba | Larghezza massima della lamina (cm) | C | larlam |
| Forma dell’apice della lamina delle FMS | D | formapi | Largh. lamina a ¼ apicale | C | baseapice |
| Colore del picciolo (FMS) | D | colopic | Angolo inserzione 2a nervatura lat. e NC. | C | angolo |
I risultati relativi ai singoli caratteri sono stati analizzati con appropriate procedure statistiche e l’ipotesi di eguaglianza dei cloni è stata statisticamente rifiutata per tutti i caratteri (dati non riportati, ma compresi in altra pubblicazione nell’ambito del sottoprogetto). La procedura Random Forest è stata applicata all’intero insieme di dati disponibili e relativi a 40 vettori - pianta per ciascun clone.
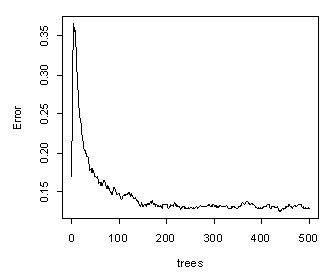
La procedura genera un numero crescente di alberi classificatori e permette stime dell’errore di generalizzazione. In Fig. 1 è riportata la percentuale di errore in funzione del numero di alberi contenuti nella foresta casuale. Già con 200 alberi l’errore si assesta a circa 0.13.
Fig. 1 - Errore di classificazione in funzione del numero di alberi contenuti nella foresta casuale.
Come tutti procedimenti di analisi discriminante, le Foreste stocastiche derivano le regole migliori per assegnare i singoli casi (nel nostro caso le singole piante) alla classe di appartenenza. La bontà del procedimento si verifica riclassificando le singole piante appartenenti al training data set sulla base delle regole classificatorie ottenute.
In Tab. 3 è riportata la matrice di confondimento ottenuta dall’output della procedura. In considerazione che la matrice ottimale è costituita nel nostro caso da una diagonale con il valore 40, possiamo osservare che la riclassificazione ottenuta è piuttosto buona, considerando che il training data set è costituito da vettori relativi a dati di singole piante allevate in due diverse località. I risultati di classificazione peggiori sono relativi al clone I-45/51 (# 11) ed al clone Triplo (# 13), entrambi Populus x canadensis, che si ripartiscono quasi al 50% le relative piante. Il clone Bellini (#18) presenta anch’esso un elevato errore, con sole 16 piante correttamente classificate sulle 37 valutate. L’errore medio di classificazione di tutti i cloni è comunque pari a 0.13 con ben 22 cloni su 30 al disotto di tale livello (Tab. 4).
Tab. 3 - Matrice di confondimento ottenuta dalla procedura di classificazione.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 36 | 0 | 1 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 35 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 0 | 30 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 1 | 0 | 33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 34 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 36 | 1 | 0 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 22 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 37 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 20 | 0 | 17 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 32 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 34 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 2 | 1 | 0 | 0 | 1 | 0 |
| 18 | 0 | 1 | 1 | 0 | 8 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 35 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 2 | 3 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 34 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 37 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 24 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 35 | 0 | 0 | 0 | 0 | 0 | 0 |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 35 | 0 | 0 | 0 | 0 | 0 |
| 26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 39 | 1 | 0 | 0 | 0 |
| 27 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 30 | 0 | 0 | 0 |
| 28 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 33 | 0 | 0 |
| 29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 39 | 0 |
| 30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 39 |
Tab. 4 - Percentuali d’errore per ciascun clone.
| Clone | Errore | Clone | Errore |
|---|---|---|---|
| 1 | 0.0250 | 16 | 0.1111 |
| 2 | 0.0250 | 17 | 0.1500 |
| 3 | 0.1000 | 18 | 0.4074 |
| 4 | 0.1026 | 19 | 0.0789 |
| 5 | 0.1429 | 20 | 0.2500 |
| 6 | 0.1750 | 21 | 0.0811 |
| 7 | 0.0811 | 22 | 0.0750 |
| 8 | 0.1250 | 23 | 0.1000 |
| 9 | 0.1000 | 24 | 0.0789 |
| 10 | 0.1000 | 25 | 0.0540 |
| 11 | 0.4500 | 26 | 0.0250 |
| 12 | 0.0750 | 27 | 0.1176 |
| 13 | 0.5750 | 28 | 0.1081 |
| 14 | 0.1250 | 29 | 0.0250 |
| 15 | 0.0250 | 30 | 0.000 |
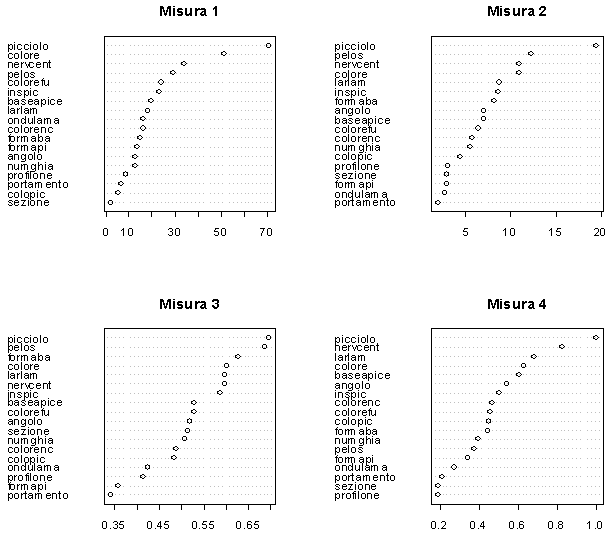
Un ulteriore vantaggio delle Foreste Casuali consiste nella possibilità di ordinare i caratteri utilizzati sulla base del loro contributo relativo al processo di classificazione. Nella Fig. 2 sono riportati graficamente i risultati relativi alle quattro misure descritte sopra.
Fig. 2 - Ordinamento delle variabili classificatrici in base al valore assunto da quattro “misure” differenti (si veda il testo).
Le variabili “portamento” (portamento delle foglie in relazione al fusto), “sezione” (sezione del fusto) e “formapi” (forma dell’apice della lamina) sono risultate poco informative pressoché con ognuna delle quattro misure. Al massimo valore per le misure si pongono “picciolo” (lunghezza del picciolo), “pelos” (pelosità del germoglio), “nervcent” (lunghezza della nervatura centrale) e “colore” (colore del germoglio apicale). Valutato convenientemente il significato delle misure proposte da Breiman è possibile identificare le variabili che sono risultate meno utili ai fini classificatori, almeno relativamente al training data set utilizzato.
Considerazioni conclusive
L’utilizzo di tecniche discriminanti sulla base di procedure di tassonomia numerica è una consolidata strategia in diversi settori della biologia applicata. Più complesso è il loro utilizzo nel caso di uso congiunto di variabili caratterizzate da diverse proprietà distributive. In questo caso i metodi di simulazione numerica possono essere di valido aiuto. Nel settore della valutazione dell’informazione molecolare evidenziata da marcatori abbiamo efficacemente utilizzato i cosiddetti Algoritmi Genetici, tecniche numeriche che propongono soluzioni ottimizzate simulando le proprietà dell’evoluzione biologica ([5]). Queste procedure presentano comunque difficoltà legate alla convergenza. Le Foreste Casuali, proposte da Breiman e qui applicate in modo originale ad un problema di classificazione e riconoscimento clonale, utilizzano strategie Monte Carlo, ma superano alcune delle limitazioni proprie degli Algoritmi Genetici.
Sulla base dei dati disponibili possiamo giudicare soddisfacente l’abilità della procedura nell’assegnare, dopo apprendimento sulla base di un data training set volutamente eterogeneo, un gruppo di piante (nel nostro caso 40) al clone di appartenenza. Con l’eccezione di tre cloni, il livello di errore riferito alla singola pianta è mediamente ridotto. Naturalmente il livello di efficienza diminuisce con le dimensioni del campione rendendo poco realistico l’utilizzo della procedura di discriminazione per assegnare al proprio clone una sola pianta. La tecnica, riferita ad un lotto di piante valutate in una singola località, può essere già agevolmente applicata anche con risorse di calcolo limitate, ponendo particolare attenzione alle tecniche di rilevamento dei caratteri, peraltro facilmente automatizzabili con l’ausilio di un calcolatore palmare.
Non va infine sottovalutato che la procedura qui descritta può essere estesa anche ad ulteriori descrittori con caratteristiche diverse e tra questi, anche se non ancora inseriti nelle procedure di valutazione ufficiale, i numerosi marcatori molecolari che le attuali tecniche di laboratorio rendono sempre più accessibili e a costi limitati. Limitando l’analisi a descrittori morfologici, l’efficienza del sistema può essere accresciuta valutando l’inserimento di nuove caratteristiche nella fase di training e considerando campioni di dimensioni più ampie per quei cloni che presentano maggiori difficoltà classificatorie.
Ringraziamenti
Lavoro svolto nell’ambito del progetto Ri.Selv.Italia, sottoprogetto 2.2 “Arboricoltura da legno con specie a rapido accrescimento (pioppicoltura)”. Gli Autori ringraziano il Dott. Stefano Bisoffi ed il personale dell’Istituto di sperimentazione per la Pioppicoltura (Casale Monferrato) per la collaborazione ed il Prof. L. Breiman per la disponibilità del software e gli utili suggerimenti forniti.
References
Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar