The Winkelmass index as a forest management tool for inventorying stand structure
Forest@ - Journal of Silviculture and Forest Ecology, Volume 2, Pages 225-232 (2005)
doi: https://doi.org/10.3832/efor0280-0020225
Published: Jun 08, 2005 - Copyright © 2005 SISEF
Research Articles
Guest Editors: RI.SELV.ITALIA - MiPAF Project
« Shared Research Program on Silviculture in Italy »
Collection/Special Issue: Massimo Bianchi
Abstract
Spatial pattern of tree species, sizes and ages affects functional processes and biodiversity of forest ecosystems. Therefore, it is more and more important that stand structural diversity can be assessed through easy-to-implement methodologies at forest management scale. This paper discusses the application of a recently proposed index (the Winkelmass index) of tree spatial aggregation, based on the measurement of the angles between neighboring stems, to a beech (Fagus sylvatica L.) forest in Northern Latium (Italy). Results shows that the Winkelmass index can be implemented in a simple and fast way according to objective sampling schemes and allows to produce a raster map of tree aggregation pattern in the forest. Under the stand condition in the test area, only four trees at each sample point were sufficient to characterize prevailing stand horizontal structure.
Keywords
Introduzione
La diversità strutturale dei popolamenti forestali rappresenta una delle principali componenti della biodiversità degli ecosistemi boschivi ([11]). Essa dipende dalla fase di sviluppo dei popolamenti ([16], [6]) ed è generalmente collegata con la varietà specifica e genetica complessiva: a esempio, vari studi hanno dimostrato l’esistenza di una correlazione positiva tra la ricchezza di specie ornitiche e l’articolazione della struttura arborea verticale ([12], [13], [3]).
La massima parte dei boschi italiani viene definita, nell’ambito del Temperate and Boreal Forest Resources Assessment (TBFRA2000; vedi [24]), come “foreste seminaturali”, cioè sistemi in cui l’azione antropica ha portato alterazioni della originaria complessità strutturale e compositiva ([8], [15]). Ciò è avvenuto soprattutto a causa di una gestione che spesso ha teso a favorire univocamente le specie di maggiore interesse economico, coltivandole in popolamenti il più possibile uniformi quanto a dimensioni ed età degli individui arborei. La biodiversità e i processi funzionali del bosco ne hanno risentito negativamente, e ciò costituisce oggi un dato di fatto a fronte dei sempre più numerosi beni e servizi che le foreste sono chiamate a fornire alla società, molti dei quali legati alla natura complessa dei sistemi boschivi. Peraltro, in Italia, i modelli gestionali proposti in sede di pianificazione, in genere tradizionalmente orientati alla cosiddetta “normalizzazione” del bosco, spesso non sono stati pedissequamente applicati e, dunque, spesso la diversità strutturale risulta, in realtà, sorprendentemente più elevata di quanto ci si potrebbe aspettare ([7], [1]).
Le nuove esigenze della gestione forestale e l’importanza acquisita dal cosiddetto “momento strutturale” della coltivazione ([7]) evidenziano l’importanza di valutare la diversità residuale relativa alle dimensioni degli alberi e al loro disporsi nello spazio. Ciò al fine di confrontare situazioni diverse e trarne informazioni di base per l’applicazione della selvicoltura in chiave sistemica. Alle descrizioni ritraibili dalle classiche elaborazioni dendrometriche, quali la curva di distribuzione delle frequenze dei diametri, delle altezze e delle età degli alberi, si sono oggi affiancate quelle offerte da numerosi indici sintetici (per un’ampia rivista, vedi [14], [23], [19], [9]). Per quanto riguarda la descrizione della struttura nello spazio orizzontale, l’applicazione pratica della gran parte di questi indici si basa su semplici misure di distanza o di posizione reciproca tra alberi vicini, effettuate in corrispondenza dei nodi di una griglia di campionamento.
Da qui la necessità di una sperimentazione, in condizioni che caratterizzano i boschi italiani, che evidenzi il rapporto tra le informazioni ottenibili da questo tipo di indici e l’impegno operativo da affrontare. Il confronto con le informazioni desumibili dai rilievi convenzionali e con altri indici di natura biologica è il primo passo per la valutazione della capacità descrittiva di un indice. Ad esso va associata un’adeguata tecnica campionaria, che ne supporti il ruolo nel descrivere oggettivamente la diversità strutturale di soprassuoli forestali.
Questo lavoro riferisce di una sperimentazione condotta in merito all’applicazione di uno degli indici più semplici e innovativi proposti a livello internazionale negli ultimi anni per la descrizione della struttura di un popolamento forestale nello spazio orizzontale: l’indice Winkelmass ([25], [26]).
L’Indice Winkelmass
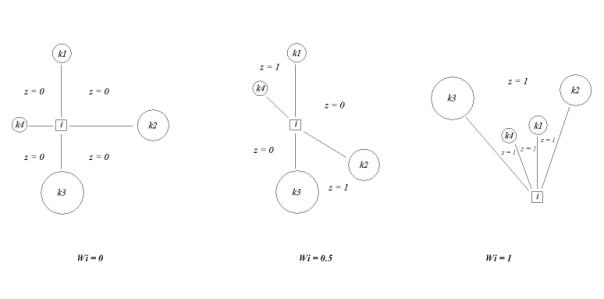
L’indice Winkelmass (W) consente di descrivere la modalità di distribuzione spaziale degli alberi in corrispondenza di un dato punto di sondaggio all’interno di un dato popolamento forestale, tramite l’osservazione degli angoli di direzione αj (con j = 1... k) rispetto ai k alberi più vicini intorno al punto di sondaggio.
Il vertice dell’angolo può essere costituito dall’albero più vicino al punto di sondaggio (tree-based Winkelmass; vedi [25], [26]) oppure dal punto di sondaggio stesso (point-or-area based Winkelmass; vedi [2]): sotto il profilo operativo, quest’ultimo approccio è in genere preferibile ([2]).
L’angolo tra due alberi vicini può essere misurato in senso orario o antiorario: in ogni caso va considerato quello di minore ampiezza. Il confronto tra il valore dell’angolo misurato αj con un valore di riferimento αr fornisce una variabile binaria zj che assume i seguenti valori (eqn. 1):
L’angolo di riferimento è pari a 1/k dell’angolo giro, valore atteso nel caso di distribuzione perfettamente regolare degli alberi.
Fig. 1 - Valori assunti dall’indice Winkelmass e dalla variabile z, nel punto di sondaggio i, con k = 4 alberi di riferimento
L’indice W, calcolato per l’i-esimo punto di sondaggio, è pari alla media del valore assunto dalla variabile zj (Fig. 1 - eqn. 2):
In caso di distribuzione regolare, valori di Wi pari a zero si hanno nel caso in cui il punto di sondaggio cada al centro del gruppo di alberi o nelle sue immediate vicinanze, rendendo minimo l’intervallo di valori di Wi che distinguono una distribuzione regolare da una casuale. Per tale motivo, all’angolo di riferimento si applica una percentuale di tolleranza che alcuni studi empirici consigliano porre uguale al 20%, cioè αr = 0.8 x α0 ([26]), con α0 pari a 1/k dell’angolo giro.
Nell’applicazione di questa procedura non è in realtà richiesta la misura diretta di nessun angolo, ma solamente la verifica della condizione espressa in eqn. 1, che può essere eseguita a vista o tramite appositi strumenti tarati sull’angolo di riferimento adottato, rendendo così il rilievo molto speditivo.
I valori che può assumere Wi variano tra 0 e 1. I valori estremi caratterizzano, rispettivamente, distribuzioni degli alberi nello spazio orizzontale di tipo regolare o a gruppi. I valori intermedi caratterizzano distribuzioni spaziali che tendono a essere casuali (Wi = 0.5).
Nel caso di campionamento casuale o sistematico semplice, lo stimatore del valore medio dell’indice Winkelmass in un dato popolamento forestale è pari a (eqn. 3):
dove n è il numero di punti di sondaggio. La variabilità di può essere stimata tramite il suo errore standard (ess), pari a (eqn. 4):
Area sperimentale
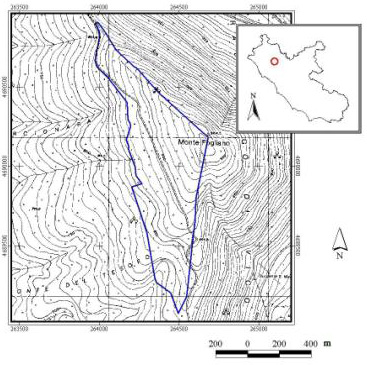
L’area oggetto di sperimentazione è situata nell’alto Lazio, sulla parte sommitale del versante occidentale di Monte Fogliano, nel territorio del Comune di Vetralla (VT). È compresa tra le quote di 780 e 960 m s.l.m., e ha una superficie complessiva di circa 50 ettari (Fig. 2).
Secondo la carta fitoclimatica del Lazio ([4]), l’area in questione rientra nella Regione Temperata, Termotipo collinare inferiore/superiore, Ombrotipo subumido superiore/umido inferiore, Regione mesaxerica (sottoregione ipomesaxerica).
La vegetazione forestale è costituita da una faggeta di quota, inquadrata nel Corydalidi-Fagetum ([5], [20]) o, secondo alcuni autori, nel Polysticho-Fagetum aceretosum pseudoplatani ([22]), dell’alleanza Fagion sylvaticae. Tale faggeta, insieme a quella più nota del Monte Cimino, è caratterizzata da termotipi più umidi e freschi rispetto alla restante parte del territorio viterbese ([21]). Accanto al faggio (Fagus sylvatica L.) sono presenti, con frequenze minori, il cerro (Quercuscerris L.), soprattutto nelle esposizioni sud-occidentali, il castagno (Castanea sativa Miller) e altre latifoglie mesofite (Acer spp., Sambucus nigra L.).
La gestione dei boschi del Comune di Vetralla si è evoluta attraverso ripetuti piani di assestamento forestale, iniziati circa sessant’anni fa ([10]) con orientamento strettamente produttivo. I successivi piani di assestamento ([17], [18]) inclusero i boschi sommitali del Monte Fogliano in una classe colturale definita “fustaia estetica” (superficie pari a circa 57 ettari), che, soggetta a vincolo paesaggistico, è rimasta nel complesso invariata fino ad oggi.
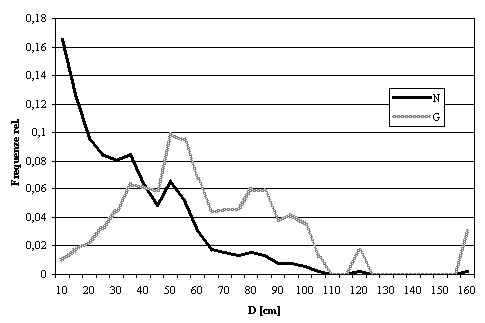
L’attuale struttura di questi popolamenti è assimilabile al classico tipo disetaneo (Fig. 3), con alberi di grosse dimensioni e con scarso sottobosco arbustivo.
Fig. 3 - Distribuzione complessiva delle frequenze relative del numero di alberi e dell’area basimetrica per classi diametriche nell’area sperimentale
Metodologia sperimentale
All’interno dell’area di studio è stato realizzato un campionamento sistematico per il rilevamento dell’indice Winkelmass, su un reticolo con passo di 50 metri appoggiato al sistema di coordinate UTM 33N ED50.
A ciascun nodo del reticolo è stato associato un punto di sondaggio, per un totale di 203 unità campionarie.
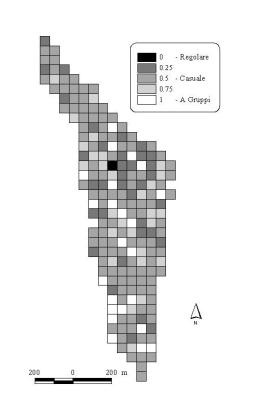
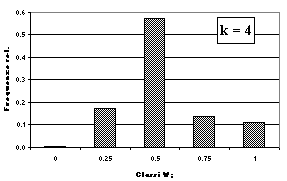
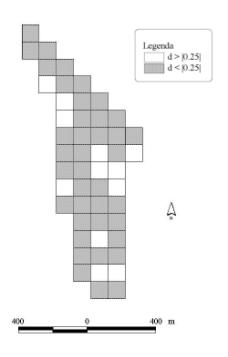
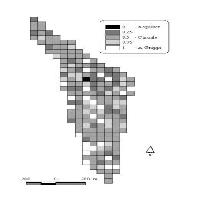
Per ciascun punto di sondaggio è stato calcolato il valore dell’indice Winkelmass con k = 4 (Wi4), ossia considerando i quattro alberi più vicini al punto di sondaggio. Sono stati considerati tutti gli alberi con diametro a petto d’uomo pari o superiore a 7.5 cm. L’indice Wi4 può assumere cinque valori: 0 - 0.25 - 0.5 - 0.75 - 1. Con i valori calcolati è stata costruita una “mappa del contagio”, che evidenzia la struttura del popolamento nello spazio orizzontale (Fig. 4).
Utilizzando lo stesso reticolo, ma adottando un passo di 100 metri (51 unità campionarie), sono stati anche calcolati i valori dell’indice Winkelmass per k = 6 (Wi6) e per k = 8 (Wi8). Wi6 può assumere sette valori (0 - 0.167- 0.333 - 0.5 - 0.667- 0.833- 1) e Wi8 nove (0 - 0.125 - 0.25 - 0.375 - 0.5 - 0.625 - 0.75 - 0.875 - 1).
Centrata attorno a ciascun punto di sondaggio ottenuto dal reticolo con passo di 100 m è stata anche delimitata un’area campione di forma quadrata, con lato pari a 20 m. In ciascuna area campione è stato eseguito il cavallettamento degli alberi presenti con diametro pari a 7.5 cm o superiore.
I valori dell’indice Winkelmass sono stati posti in correlazione con i parametri dendrometrici derivanti dal cavallettamento e con l’indice di diversità strutturale H’ ([23]) determinato in base al numero di alberi e all’area basimetrica di ciascuna classe diametrica (eqn. 5):
dove Ni è il numero totale di alberi cavallettati (oppure area basimetrica totale) nell’i-esima area campione; nij è il numero di alberi (o area basimetrica) afferenti alla j-esima classe diametrica nella i-esima area campione; Si è il numero di classi diametriche nella i-esima area campione.
L’indice H’ misura la diversità di distribuzione del numero di alberi (o dell’area basimetrica) nelle diverse classi diametriche. Tale diversità risulta massima quando tutte le classi diametriche hanno lo stesso numero di alberi (o lo stesso valore di area basimetrica): in questo caso, il valore assunto dall’indice H’ sarà pari al logaritmo naturale di S. Il rapporto tra l’indice H’ e il suo valore massimo teorico viene chiamato indice di uniformità ([14], [9] - eqn. 6):
La correlazione tra indici e parametri dendrometrici è stata quantificata tramite il coefficiente di correlazione di Pearson, secondo la seguente formula (eqn. 7):
dove: s2xy è la covarianza stimata degli attributi; sx è la deviazione standard stimata per l’attributo x; sy è la deviazione standard stimata per l’attributo y.
Risultati
Nelle Fig. 3 e Fig. 5 sono evidenziate la distribuzione complessiva del numero di piante per classi diametriche e la distribuzione complessiva del numero di piante e dell’area basimetrica per specie, così come risultano dal cavallettamento delle 51 aree campione. Il numero medio di alberi ad ettaro è pari a 255, con diametro medio pari a 40.6 cm.
Fig. 5 - Distribuzione percentuale del numero di piante (N) e dell’area basimetrica (G) per specie nell’area sperimentale
Il valore medio dell’indice Winkelmass calcolato con quattro alberi di riferimento (k = 4, 203 osservazioni) è risultato pari a 0.546 (ess% = 2.8%) (Fig. 6). All’interno del popolamento prevale quindi una distribuzione degli alberi di tipo casuale; nella parte centrale e verso l’estremità sud dell’area di studio la struttura tende comunque a essere diversa, con distribuzione delle piante a tratti più raggruppata, a tratti più uniforme (Fig. 4).
Il confronto tra i valori medi dell’indice Winkelmass calcolato per k pari a 4, 6 e 8 è riportato in Tab. 1. L’indice assume valori medi molto simili, senza differenze significative: ciò dimostra che, in condizioni analoghe a quelle esaminate, per la determinazione dell’indice Winkelmass a livello di particella forestale non è necessario utilizzare più di quattro alberi per ciascun punto di sondaggio. Ovviamente, la scelta di 4, 6 o 8 alberi fa variare il valore dell’indice W in ciascun punto di sondaggio; le differenze di valori rilevati per l’indice calcolato tra 4 e 6 alberi, tra 6 e 8 alberi e tra 4 e 8 alberi, in ciascun punto di sondaggio, sono però nel 76.5% dei casi inferiori a |0.25| (Fig. 7).
Tab. 1 - Valori medi dell’indice Winkelmass al variare di k nell’area sperimentale (numero di osservazioni = 51).
| Numero di alberi utilizzati (k) | Valore medio dell’indice W | Errore standard dell’indice W |
|---|---|---|
| 4 | 0.559 | 0.028 |
| 6 | 0.526 | 0.023 |
| 8 | 0.529 | 0.021 |
Nella Tab. 2 sono riportati i valori medi dell’indice Winkelmass (per k = 4) calcolati su un numero crescente di unità campionarie (51, 101, 203, corrispondenti rispettivamente a reticoli con passo di 50, 71 e 100 m). Nelle condizioni esaminate, i valori medi dell’indice risultano indipendenti dalla numerosità del campione, e presentano ovviamente valori di errore standard che diminuiscono all’aumentare della numerosità del campione.
Tab. 2 - Valori medi dell’indice Winkelmass (con k = 4) nell’area sperimentale al variare della numerosità campionaria.
| Numerosità del campione | Valore medio dell’indice W | Errore standard dell’indice W |
|---|---|---|
| 51 | 0.559 | 0.028 |
| 101 | 0.535 | 0.020 |
| 203 | 0.546 | 0.015 |
Il valore medio dell’indice H’, calcolato per il numero degli alberi ad ettaro (H’N), con classi diametriche di ampiezza di 5 cm, è pari a 1.594, mentre il valore medio stimato per l’area basimetrica (H’G) è pari a 1.388. L’indice di uniformità, calcolato per il numero degli alberi ad ettaro (EN), è pari a 0.939, mentre il valore stimato per l’area basimetrica (EG) è pari a 0.817.
Mediamente, l’indice H’ indica una diversità strutturale lievemente maggiore in termini di numero di alberi per classi diametriche; nel complesso, tale diversità risulta elevata, con valori prossimi al massimo teorico, come dimostrato dai valori dell’indice di uniformità.
Dalla Tab. 3 risulta evidente la completa indipendenza dell’indice Winkelmass rispetto a tutti gli altri parametri misurati nell’area sperimentale.
Tab. 3 - Coefficiente di correlazione dell’indice Winkelmass rispetto agli altri parametri misurati nell’area sperimentale (numero di osservazioni = 51).
| - | Indice EN | Indice EG | Indice H’N | Indice H’G | Numero alberi a ettaro |
Area basimetrica a ettaro |
|---|---|---|---|---|---|---|
| Valore | -0.009 | -0.033 | -0.117 | -0.137 | -0.040 | -0.150 |
Discussione e conclusioni
L’indice di aggregazione Winkelmass descrive il tipo di distribuzione spaziale di k alberi attorno a un dato punto di sondaggio. Implementato nel contesto di un disegno campionario probabilistico, esso permette di descrivere in modo agevole e oggettivo le caratteristiche strutturali dei popolamenti forestali nello spazio orizzontale, utili ai fini di descrizione particellare in ambito assestamentale, in associazione alle convenzionali metodologie dendrometriche.
La possibilità di creare una mappa della struttura spaziale orizzontale dei fusti arborei consente la realizzazione di uno strato informativo raster utile anche direttamente a fini gestionali.
La sperimentazione condotta ha evidenziato come l’indice Winkelmass sia di facile e veloce rilievo in bosco, non richiedendo misurazioni dirette né delle distanze, né degli angoli tra i k alberi considerati. L’accertata possibilità di eseguire il rilievo con riferimento a solo 4 alberi intorno a ciascun punto di sondaggio consente, in condizioni analoghe a quelle esaminate, di accelerare ulteriormente i tempi di rilievo.
Come atteso, i valori dell’indice Winkelmass sono risultati indipendenti sia nei confronti di parametri dendrometrici convenzionali, sia nei confronti di indici di diversità strutturale calcolati sulla ripartizione degli alberi per classi diametriche: ne va pertanto sottolineata la rilevanza applicativa in quanto fornisce un differente contributo alla descrizione quantitativa dell’eterogeneità strutturale dei soprassuoli forestali, mettendone in risalto specifiche peculiarità.
Ringraziamenti
Lavoro svolto in parti uguali dagli autori, nell’ambito del progetto Ri.Selv.Italia, sottoprogetto 4.2 “Sistemi Informativi di Supporto per la Gestione Forestale”.
References
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar