Comparison between parametric and non-parametric methods for the spazialization of forest standing volume by integrating field measures, remote sensing data and ancillary data
Forest@ - Journal of Silviculture and Forest Ecology, Volume 4, Pages 110-117 (2007)
doi: https://doi.org/10.3832/efor0439-0040110
Published: Mar 21, 2007 - Copyright © 2007 SISEF
Research Articles
Guest Editors: 5° SISEF Congress (Grugliasco, TO - 2005)
« Forests and Society - Changes, Conflicts, Sinergies »
Collection/Special Issue: E. Lingua, R. Marzano, G. Minotta, R. Motta, A. Nosenzo, G. Bovio
Abstract
The use of remotely sensed data for forest inventory and monitoring of natural resources is ever increasing. Distinctively, remotely sensed data, integrated with ancillary data, can be exploited for the spazialization of biophysical attributes measured by forest inventories or management plans. Such applications are based on the relationships between the considered attributes and the spectral information measured by multispectral satellite images. Operative applications are commonly based on parametric or, more frequently, non-parametric approaches. The final aim of the present contribution is the spazialization of forest standing volume of various tree species in a study site in northern Italy by parametric (multiregressive) and non-parametric algorithms (k-Nearest Neighbors). The project is based on field data measured in productive forest stands dominated by Abies alba Mill. and/or Picea abies L. in the Provincia Autonoma di Trento (eastern Alpine Region of Italy). Remotely sensed images were acquired by the Landsat 7 ETM+ sensor while ancillary information is given by the altitude obtained from DEM and the site fertility from the GIS of the management plans. The contribution compares spazialization performance of several operative configurations of the tested methods in order to provide guidelines for the operative application of such techniques on vast areas. The study results emphasize the higher suitability of the tested non-parametric methods.
Keywords
Forest management, Forest mapping, Spazialization, Multiregressive method, k-nearest neighbors method
Introduzione
Il crescente interesse verso le problematiche ambientali ha generato l’esigenza di ampliare e approfondire le conoscenze sui sistemi naturali e semi-naturali ([3]). Per quanto riguarda il settore forestale si registra una crescita del numero e del tipo di attributi misurati nell’ambito di indagini inventariali ([5], [8], [6], [22]), anche grazie allo sviluppo di strumenti, metodi e tecniche di rilievo sempre più sofisticati.
Tuttavia permane il problema legato ai costi di rilevamento. Indipendentemente dalla scala e dalla finalità di indagine (inventari forestali, piani di assestamento e di gestione forestale, ecc.), le misure in bosco richiedono tempi medi di esecuzione relativamente lunghi, per cui, in genere, si preferisce sempre più limitare le operazioni di campagna a un numero rappresentativo di unità di campionamento a terra, ricorrendo poi all’uso di stimatori per derivare una o più informazioni sull’intera popolazione di riferimento. Quando l’obiettivo è la stima di un valore dell’attributo di interesse per ciascuna unità della popolazione, come avviene per le applicazioni cartografiche di tipo quantitativo, questa operazione viene detta spazializzazione, cioè estensione in modo continuo a un intero territorio di dati rilevati a terra a livello puntuale (ad esempio, in aree di saggio).
I metodi di spazializzazione che trovano maggiore utilizzo ed efficacia in cartografia forestale sono soprattutto quelli di tipo correlativo ([2]). Questi metodi fanno ricorso a funzioni analitiche che quantificano la relazione esistente tra la variabile dipendente (attributo oggetto di interesse) misurata su un campione della popolazione e una o più variabili indipendenti (dati ancillari) note su tutta la popolazione attraverso banche dati geografiche e/o acquisite con applicazioni di telerilevamento. Tra le principali tecniche sviluppate in questo ambito si ricordano quelle di tipo parametrico, per rapporto o per regressione lineare ([4]), e quelle di tipo non-parametrico, basate sulle distanze dai prossimi più vicini (k Nearest Neighbors,k-NN; [20], [21], [1]).
In questo lavoro vengono presentati e discussi i risultati ottenuti dal confronto della spazializzazione effettuata con metodo parametrico (regressione lineare) e non-parametrico (k-NN) dell’attributo provvigione legnosa unitaria (espressa in m3 ha-1) su una popolazione di particelle forestali omogenee per tipo forestale e indirizzo gestionale, in un’area di studio dell’Italia settentrionale. Il protocollo sperimentale è stato impostato in modo da poter valutare comparativamente, in termini di accuratezza delle stime prodotte, diverse configurazioni degli algoritmi di spazializzazione, al fine di fornire indicazioni per applicazioni operative su vasti territori.
Metodi correlativi di spazializzazione
Di seguito vengono sinteticamente illustrate le modalità applicative dei metodi di spazializzazione esaminati nell’ambito del presente contributo: per maggiori dettagli, si rimanda a Chirici & Corona ([2]).
Spazializzazione per regressione
Il metodo regressivo ai fini della spazializzazione di un dato attributo forestale richiede: (i) una discretizzazione del territorio indagato in tessere, che rappresentano le unità della popolazione per ciascuna delle quali sono disponibili i dati ancillari (variabili indipendenti ottenute da banche dati geografiche esistenti e/o acquisite con tecniche di telerilevamento) e per le quali deve essere predetto il valore dell’attributo considerato (variabile indipendente); (ii) l’estrazione di alcune tessere campione; (iii) il rilievo in campo dell’attributo d’interesse in corrispondenza delle tessere campione.
Sulla base dell’analisi condotta nelle tessere campione viene quindi istituita una regressione tra la variabile dipendente, rappresentata dai valori noti dell’attributo oggetto d’interesse, e la/e variabile/i indipendente/i. L’equazione di regressione è poi utilizzata per la stima dell’attributo considerato su tutte le tessere del territorio indagato.
Spazializzazione con metodo k-NN
Il metodo di stima k-NN prevede inizialmente le stesse operazioni di cui ai punti (i)-(iii) del paragrafo precedente.
La stima dell’attributo considerato per ogni tessera con valore incognito (p0) viene quindi effettuata ricercando le k tessere ad essa più simili tra quelle corrispondenti alle unità di rilevamento a terra (pi): questa operazione richiede il calcolo della distanza tra la tessera con valore incognito e tutte le altre n tessere con valori noti dell’attributo (pi) misurata in uno spazio multidimensionale definito dalle variabili indipendenti considerate. I valori dell’attributo (mpi) rilevato in corrispondenza delle k tessere più vicine sono utilizzati per la stima dell’attributo sulla tessera con valore incognito, ottenuta come media (Mp0) dei k valori pesati sull’inverso della suddetta distanza multidimensionale, in modo da assegnare alle tessere più vicine un peso maggiore (eqn. 1):
dove wpi p0 è il peso attribuito alla tessera campione pi (con valori noti dell’attributo considerato) rispetto alla tessera p0; mpi è il valore dell’attributo misurato a terra in corrispondenza della tessera pi (eqn. 2);
dove dpi p0 = distanza multidimensionale tra la tessera campione pi e la tessera con p0.
La distanza multidimensionale viene valutata in base alle variabili indipendenti considerate, costituite in genere dalla riflettanza nelle singole bande spettrali di immagini telerilevate, da indici ottenuti per combinazione tra le bande e da altre variabili ancillari che descrivono i caratteri della stazione, come la quota, la classe di fertilità, ecc. ([12], [15], [9]). È possibile limitare la scelta delle k tessere più vicine a quelle geograficamente più vicine alla tessera con valore incognito (p0) o che rientrano in un intervallo altimetrico prefissato rispetto ad essa ([11]).
I sistemi sviluppati per calcolare la distanza multidimensionale sono molteplici ([7], [16]). Quelli testati in questo studio fanno riferimento alla distanza euclidea, alla distanza di Mahalanobis e alla distanza pesata con pesi fuzzy.
La migliore configurazione dell’algoritmo k-NN, in termini di distanza multidimensionale e numero di k ottimali, è individuata attraverso una procedura di validazione incrociata (cross-validation) applicata con riferimento alle tessere con valori noti dell’attributo di interesse. In particolare, in questo studio viene utilizzata la procedura di validazione leave one out ([11]), che produce in output lo scarto quadratico medio (RMSE - root mean square error) e il coefficiente di correlazione (r) calcolati confrontando il valore dell’attributo (mpi) misurato a terra in corrispondenza di una data tessera campione (pi), con il valore (Mpi) stimato sulla stessa con metodo k-NN calibrato escludendo nel processo di calibrazione il valore vero di quella stessa tessera.
Materiali
Il protocollo sperimentale è stato testato in Provincia di Trento, utilizzando l’Archivio Generale dei Piani Economici Forestali della Provincia aggiornato al 2000.
L’Archivio è costituito da un Sistema Informativo Territoriale che per ogni particella forestale, oltre a indicare la posizione sul territorio e il codice del piano di assestamento di appartenenza, riporta la descrizione dei principali caratteri della stazione (quota, classe di fertilità, ecc.), del soprassuolo (destinazione, forma di governo, composizione specifica, area basimetrica, provvigione legnosa, ecc.) e il tipo di rilievo previsto dal relativo piano (cavallettamento totale, aree di saggio, ecc.).
Come dato telerilevato è stata utilizzata una scena multispettrale del satellite Landsat 7 ETM+ (path 193, row 028), acquisita nell’estate del 2000.
Le bande multispettrali Landsat con risoluzione geometrica di 30 m sono state ortocorrette utilizzando ortofoto digitali AIMA a 8 bit per il posizionamento dei GCPs (Ground Control Points) e un modello digitale del terreno con passo di 75 m. L’errore quadratico medio commesso nella procedura di ortorettifica è risultato inferiore alla dimensione del pixel. Il ricampionamento delle immagini è stato eseguito con metodo nearest neighbor ([14]).
Poiché in aree orograficamente complesse la variabilità delle condizioni di illuminazione del terreno può costituire una significativa fonte di errore, per valutare gli effetti dell’orografia sull’accuratezza delle stime prodotte le bande multispettrali Landsat sono state normalizzate topograficamente con il metodo C-factor ([19], [10], [18]).
Protocollo sperimentale
Definizione della popolazione di riferimento
In questo studio sono prese in esame le fustaie a destinazione produttiva con una percentuale di abete bianco (Abies alba Mill.) e/o abete rosso (Picea abies L.) superiore al 50%, sottoposte a rilievo diretto tramite cavallettamento totale.
Interrogando il database geografico dei Piani Economici Forestali è risultato che 1097 particelle rispondevano ai requisiti elencati. Di queste ne sono state scartate 33 particelle perché prive della copertura satellitare utilizzata e 748 particelle perché l’anno di aggiornamento del rispettivo piano è risultato più vecchio di cinque anni rispetto all’anno di acquisizione della scena Landsat. La scelta di una soglia differenziale massima di cinque anni è derivata dalla congiunta esigenza di dati a terra quanto più possibile coevi rispetto alle immagini telerilevate e di un numero sufficientemente ampio di osservazioni.
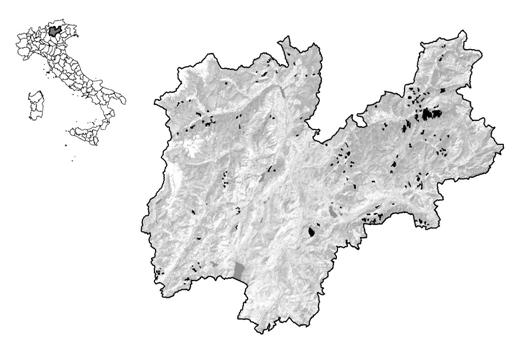
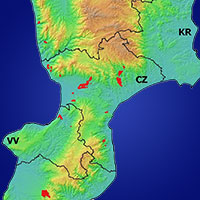
La popolazione sperimentale di riferimento è quindi rappresentata da un totale di 316 particelle forestali, che sommano complessivamente una superficie pari a 6220 ettari, distribuite a quote comprese tra 400 m s.l.m. e 1540 m s.l.m. (Fig. 1). La superficie della più piccola particella considerata è pari a 0.5 ha. La provvigione legnosa unitaria minima, massima e media riscontrata nelle 316 particelle esaminate è, rispettivamente, pari a 61 m3 ha-1, 761 m3 ha-1 e 315 m3 ha-1.
Fig. 1 - Nell’immagine in alto a sinistra è riportata la localizzazione dell’area di studio. Nell’immagine a destra è rappresentata la distribuzione geografica delle 316 particelle forestali prese in esame. Sullo sfondo è visualizzata una delle bande multispettrali del satellite Landsat 7 ETM+ mascherata sui confini amministrativi delle Provincia di Trento.
Scelta delle variabili indipendenti
Nella scelta delle variabili indipendenti è stato tenuto conto sia della necessità di avere informazioni disponibili su tutta la popolazione di riferimento, e comunque facilmente acquisibili in sede di descrizione particellare, sia del modo con cui queste sono relazionate alla variabile dipendente (nel caso specifico, alla provvigione legnosa unitaria, espressa in m3 ha-1). Infatti, maggiore è la correlazione, maggiore è la capacità di predizione dello stimatore, anche se nel caso di un approccio non-parametrico altri fattori concorrono alla determinazione del risultato finale, come il tipo di distanza tra i k nearest neighbors o il numero di k ([13]).
Le variabili indipendenti utilizzate in questo studio sono derivate sia dai valori di riflettanza nelle singole bande misurati dal sensore satellitare Landsat 7 ETM+, sia da indici ottenuti per combinazioni tra le bande, sia da semplici attributi descrittivi (altitudine media, massima e classe di fertilità della particella) derivati dai piani di assestamento forestale, secondo quanto riportato dall’Archivio Generale dei Piani Economici Forestali della Provincia di Trento (Tab. 1). Le variabili acquisite da telerilevamento sono state ottenute a livello di particella forestale come media dei valori di digital number misurati per ciascuna banda considerata nei pixel inclusi in ciascuna particella.
Tab. 1 - Variabili indipendenti (variabili ancillari) acquisite su tutte le particelle forestali esaminate.
| Codice variabile | Variabili indipendenti |
|---|---|
| 1 | Media TM1 |
| 2 | Media TM2 |
| 3 | Media TM3 |
| 4 | Media TM4 |
| 5 | Media TM5 |
| 6 | Media TM7 |
| 7 | Media IRI = (TM4-TM5)/(TM4+TM5) |
| 8 | Altitudine media |
| 9 | Altitudine massima |
| 10 | Classe di fertilità |
Dati di training e dati di validazione
Dalla popolazione di particelle indagata è stato estratto casualmente un campione di particelle (training set) per le quali il valore di provvigione legnosa è stato considerato noto sulla base dei rilievi a terra per cavallettamento totale e che è servito per calibrare, e nel caso del k-NN anche per configurare, gli algoritmi di stima.
L’affidabilità dei risultati degli algoritmi di stima così calibrati è stata verificata sulle restanti particelle (validation set, pari al 70% della numerosità della popolazione), per le quali pure era noto il valore di provvigione legnosa sulla base dei rilievi a terra per cavallettamento totale.
I valori della provvigione a ettaro minima, massima e media effettiva nelle particelle del training set e del validation set sono riportati in Tab. 2.
Tab. 2 - Provvigione legnosa unitaria minima, massima e media nelle particelle di training e di validazione.
| Set di dati | Dimensione del campione rispetto alla popolazione % | Provvigione legnosa unitaria | ||
|---|---|---|---|---|
| minima | massima | media | ||
| m3 ha-1 | m3 ha-1 | m3 ha-1 | ||
| Set di training | 10 | 158 | 568 | 312 |
| 20 | 127 | 568 | 308 | |
| 30 | 61 | 624 | 312 | |
| Set di validazione | 70 | 61 | 761 | 317 |
Tesi a confronto
Gli algoritmi di stima sono stati configurati in modo da valutare comparativamente gli effetti sul grado di accuratezza delle stime stesse relativamente a (Tab. 3):
Tab. 3 - Elenco delle 12 prove effettuate utilizzando differenti configurazioni degli algoritmi di stima. (*) swr = metodo parametrico per regressione lineare; k-NN = metodo non-parametrico per k nearest neighbors. (**) Per la decodifica delle variabili indipendenti fare riferimento alla Tab. 1. (***) E: distanza euclidea, M: distanza di Mahalanobis, PF: distanza pesata con pesi fuzzy.
| Codice tesi |
Metodo di spazializzazione* |
Normalizzazione topografica | Particelle training |
Variabili indipendenti** |
k | Distanza*** |
|---|---|---|---|---|---|---|
| % | codice | tipo | ||||
| 1 | k -NN | nessuna | 10 | tutte | 1-20 | E, M, PF |
| 2 | k -NN | nessuna | 20 | tutte | 1-20 | E, M, PF |
| 3 | k -NN | nessuna | 30 | tutte | 1-20 | E, M, PF |
| 4 | k -NN | C-factor | 10 | tutte | 1-20 | E, M, PF |
| 5 | k -NN | C-factor | 20 | tutte | 1-20 | E, M, PF |
| 6 | k -NN | C-factor | 30 | tutte | 1-20 | E, M, PF |
| 7 | swr | nessuna | 10 | 5, 10 | - | - |
| 8 | swr | nessuna | 20 | 5, 8, 10 | - | - |
| 9 | swr | nessuna | 30 | 5, 8, 10 | - | - |
| 10 | swr | C-factor | 10 | 1, 10 | - | - |
| 11 | swr | C-factor | 20 | 1, 8, 10 | - | - |
| 12 | swr | C-factor | 30 | 1, 3, 6, 8, 9, 10 | - | - |
- metodo di spazializzazione (parametrico multiregressivo o non-parametrico k-NN);
- presenza o assenza di normalizzazione topografica sulle immagini Landsat;
- dimensione del campione di training (tre dimensioni: 10%, 20%, 30% del totale di particelle).
Relativamente al metodo k-NN, è stato inoltre comparato l’effetto dell’utilizzo di valori crescenti di k (1-20) e di tre differenti tipi di distanza multidimensionale: (i) euclidea, (ii) di Mahalanobis, (iii) pesata con pesi fuzzy.
Procedure di stima e valutazione dell’accuratezza
La stima con metodo parametrico è stata eseguita con una procedura step-wise regression (swr) sulle variabili indipendenti elencate in Tab. 1 (probabilità F per inserimento = 0.05, rimozione = 0.1). In questo modo sono state calcolate le equazioni di regressione multipla con le quali estendere il dato di provvigione legnosa unitaria dalle particelle training alle particelle di validazione, con e senza normalizzazione topografica della scena satellitare e secondo tre differenti dimensioni del campione di training (10%, 20%, 30%).
La stima con metodo non-parametrico è stata sviluppata secondo l’approccio k-NN. In questo caso si è proceduto inizialmente a individuare le migliori performance di stima attraverso la procedura di validazione incrociata leave one out applicata alle particelle di training, ricercando il tipo di distanza multidimensionale e il numero k di particelle che minimizzano lo scarto quadratico medio. Stabiliti così il tipo di distanza e il valore di k ottimali, l’algoritmo è stato impostato per stimare i valori di provvigione legnosa unitaria sulle particelle di validazione (validation set).
Dal confronto tra i valori predetti di provvigione legnosa unitaria sulle particelle di validazione e quelli osservati con rilievo diretto sulle stesse particelle sono stati calcolati i seguenti indicatori di accuratezza delle stime: scarto medio, scarto quadratico medio, coefficiente di correlazione tra valori predetti e osservati.
Risultati
Configurazione dell’algoritmo k-NN
Il risultato delle migliori prestazioni ottenute con metodo k-NN applicato alle particelle di training con procedura leave one out è riportato in Tab. 4.
Tab. 4 - Migliori configurazioni dell’algoritmo k-NN ottenute con procedura di validazione incrociata di tipo leave one out applicata alle particelle di training. (*) PF: distanza pesata con pesi fuzzy; (**) Indicatori ottenuti dal confronto tra valori predetti e valori osservati sul set di training.
| Codice tesi |
Normalizzazione topografica |
Particelle training % |
k | Distanza* tipo |
Coefficiente di correlazione** |
Scarto quadratico medio** (m3 ha-1) |
|---|---|---|---|---|---|---|
| 1 | nessuna | 10 | 3 | PF | 0.786 | 70.8 |
| 2 | nessuna | 20 | 10 | PF | 0.817 | 70.1 |
| 3 | nessuna | 30 | 3 | PF | 0.809 | 75.1 |
| 4 | C-factor | 10 | 12 | PF | 0.835 | 79.5 |
| 5 | C-factor | 20 | 11 | PF | 0.842 | 65.9 |
| 6 | C-factor | 30 | 14 | PF | 0.823 | 77.0 |
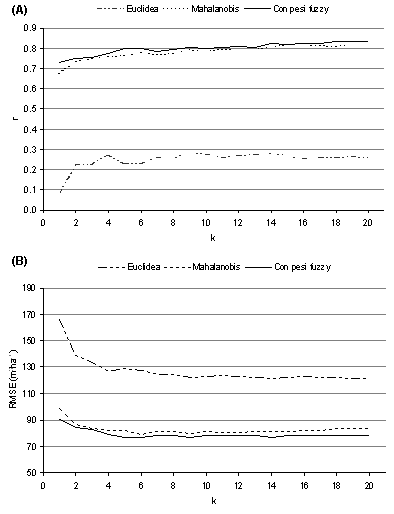
Le migliori performance si sono avute utilizzando la distanza pesata con pesi fuzzy, sebbene con risultati simili a quelli prodotti con la distanza di Mahalanobis (Fig. 2). La distanza euclidea ha fornito i risultati peggiori in tutte le prove effettuate. Tale comportamento è da attribuire al fatto che, mentre la distanza euclidea considera solo la distanza geometrica tra le unità campione e le unità target nello spazio multidimensionale definito dalle variabili indipendenti, la distanza di Mahalanobis tiene conto anche delle possibili inter-relazioni tra le suddette variabili. La distanza pesata con pesi fuzzy, invece, attribuendo un peso maggiore alle bande più informative sull’attributo in esame, in genere permette di avere prestazioni superiori ai metodi convenzionali ([16], [17]).
Fig. 2 - Esempio di output (A: coefficiente di correlazione tra valori predetti e valori osservati, B: scarto quadratico medio) della procedura di validazione incrociata leave one out applicata alle particelle di training per la configurazione dell’algoritmo k-NN. Si fa riferimento a una dimensione del campione pari al 30% della popolazione di particelle esaminate e a bande multispettrali del satellite Landsat 7 ETM+ corrette topograficamente con metodo C-factor. Sono considerati differenti tipi di distanza (euclidea, di Mahalanobis, pesata con pesi fuzzy) e valori crescenti di k (1-20).
In termini di k i migliori risultati ottenuti si sono avuti con valori compresi tra 3 e 14, confermando quanto segnalato da altri Autori in prove comparative similari ([7]).
Validazione delle stime
I risultati complessivi della verifica indipendente delle stime condotta sul validation set per ciascuna delle tesi elencate al paragrafo “Tesi a confronto” sono riportati in Tab. 5.
Tab. 5 - Risultati di validazione delle stime della provvigione legnosa unitaria per ciascuna delle tesi esaminate. Nelle tesi riferite al metodo k-NN la configurazione dell’algoritmo di stima è quella riportata in Tab. 4; nelle tesi riferite al metodo swr la configurazione dell’algoritmo di stima è quella riportata in Tab. 3.
| Codice tesi | Metodo di spazializzazione | Normalizzazione topografica |
Particelle training (%) |
K | Coefficiente di correlazione tra valori osservati e stimati (m3 ha-1) |
Scarto quadratico medio (m3 ha-1) | Scarto medio (m3 ha-1) |
Campo di variazione dei valori predetti (m3 ha-1) |
|---|---|---|---|---|---|---|---|---|
| 1 | k -NN | nessuna | 10 | 3 | 0.694 | 94.3 | 4.8 | 173-542 |
| 2 | k-NN | nessuna | 20 | 10 | 0.787 | 84.8 | 3.6 | 205-487 |
| 3 | k -NN | nessuna | 30 | 3 | 0.768 | 84.2 | 6.7 | 63-576 |
| 4 | k -NN | C-factor | 10 | 12 | 0.818 | 90.5 | 8.6 | 234-472 |
| 5 | k -NN | C-factor | 20 | 11 | 0.817 | 82.2 | 6.1 | 208-488 |
| 6 | k -NN | C-factor | 30 | 14 | 0.825 | 78.9 | 1.2 | 192-495 |
| 7 | swr | nessuna | 10 | - | 0.762 | 84.7 | -3.4 | 96-527 |
| 8 | swr | nessuna | 20 | - | 0.786 | 82.1 | -12.8 | 80-491 |
| 9 | swr | nessuna | 30 | - | 0.805 | 77.8 | -6.8 | 76-517 |
| 10 | swr | C-factor | 10 | - | 0.785 | 81.9 | -3.2 | -49-542 |
| 11 | swr | C-factor | 20 | - | 0.823 | 75.5 | -9.8 | 28-523 |
| 12 | swr | C-factor | 30 | - | 0.838 | 72.2 | -12.2 | 70-558 |
Per quanto riguarda l’effetto della dimensione del campione di training, si registra, come atteso, un leggero miglioramento dell’accuratezza di stima all’aumentare del numero di osservazioni a terra: quando si adotta una dimensione campionaria massima (30%) rispetto a quella minima testata (10%), lo scarto quadratico medio (media degli scarti quadratici tra valori osservati e valori stimati per le particelle di validazione) si riduce dell’11% con il metodo k-NN e dell’8% con il metodo regressivo.
Per quanto riguarda gli effetti dell’orografia sulle immagini telerilevate da satellite, nelle condizioni esaminate la normalizzazione topografica delle bande multispettrali ha prodotto stime di poco più accurate: adottando una dimensione del campione pari al 30%, si registra una riduzione dello scarto quadratico medio del 5% con il metodo k-NN e del 7% con il metodo regressivo rispetto a quello ottenuto con gli stessi metodi ma con immagini non normalizzate.
I valori medi di scarto tra valori osservati e valori stimati di provvigione legnosa unitaria sono relativamente contenuti, se si tiene conto che si tratta di una validazione indipendente, aggirandosi mediamente intorno al -2-3% nel caso del metodo regressivo e al +1-2% per il metodo k-NN. Le differenze tra le tesi testate non risultano comunque significative, secondo il test HSD di Tukey (α = 0.05).
Peraltro, il metodo k-NN presenta il vantaggio di fornire stime dell’attributo considerato che rientrano sempre nel campo di variabilità riscontrato in fase di campionamento a terra, a differenza di quanto avviene con il metodo regressivo, per il quale in taluni casi della tesi 10 sono state ottenute stime di provvigione legnosa unitaria anche di segno negativo.
Considerazioni conclusive
La sperimentazione condotta in provincia di Trento su una popolazione di particelle forestali a destinazione produttiva a prevalenza di abete bianco e/o abete rosso evidenzia potenzialità e limiti dei metodi testati ai fini della spazializzazione dei valori di provvigione legnosa unitaria attraverso l’integrazione di misure a terra, dati telerilevati e informazioni ancillari.
In particolare, nelle condizioni esaminate pur non avendo riscontrato differenze rilevanti tra le tesi messe a confronto, i risultati ottenuti farebbero propendere per l’uso dei metodi non-parametrici (k-NN) rispetto a quelli parametrici (metodo di stima per regressione), in quanto capaci di fornire stime dell’attributo ricercato con scarti relativamente compatibili con un utilizzo a fini operativi e con valori che rientrano nell’intervallo di variazione registrato in fase di rilievo terra.
Da un punto di vista applicativo, il metodo k-NN potrebbe rendersi utile per l’aggiornamento dei piani di assestamento e di gestione forestale. In questo caso, e con riferimento alla predizione della provvigione legnosa unitaria, è comunque opportuno:
- realizzare una stratificazione delle particelle forestali, a esempio per tipo forestale;
- adottare una dimensione del campione pari ad almeno 1/3 del numero totale di particelle forestali;
- selezionare le unità di campionamento in modo da coprire l’effettivo campo di variabilità dell’attributo considerato all’interno dell’area d’indagine;
- utilizzare metodi di calcolo della distanza multidimensionale capaci di esaltare l’importanza delle bande più informative per l’attributo oggetto di interesse;
- utilizzare bassi valori di k (3-15) per evitare un eccessivo livellamento delle stime prodotte a livello di singole particelle;
- valutare la necessità di operare la normalizzazione topografica delle immagini telerilevate in ambiti forestali ad orografia complessa e accidentata.
References
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar