Equations for the prediction of tree phytomass in Quercus cerris stands in Tuscany, Italy
Forest@ - Journal of Silviculture and Forest Ecology, Volume 4, Pages 204-212 (2007)
doi: https://doi.org/10.3832/efor0449-0040204
Published: Jun 19, 2007 - Copyright © 2007 SISEF
Research Articles
Abstract
The paper reports the development of allometric equations to estimate tree phytomass in Turkey oak stands in Tuscany. Biomass estimation is a basic tool to study the ecosystem, which is currently taking on a greater importance due to the commitments provided by the Climate Convention and the Kyoto Protocol. The high costs of the field measurements of tree biomass calls for the application of indirect methods, such as the largely-applied biomass equations, allowing to calculate phytomass values using variables easily measurable in the field, such as tree diameter and height. The equations described here have been developed for Turkey oak coppices undergoing conversion into high forests. Such stands are nowadays more and more common because of the progressive suspension of timber harvesting on an increased part of the original coppice area. We report five equations: the first one to estimate stem volume, and the followings to estimate each phytomass component (stem, branches, and slash) and the total tree above-ground phytomass. Tree diameter at breast height and total tree height were used as independent variables (predictors). All equations were developed on the same model and the additivity of the phytomass components in respect to the total phytomass was achieved. Equation parameters showed a fairly good accuracy in the estimation of the dependent variables.
Keywords
Quercus cerris, Stand biomass, Allometric equation, Biomass prediction
Introduzione
Le procedure di misurazione e di stima dell’accrescimento e della massa arborea (tavole stereometriche) si sono sviluppate in parallelo alle esigenze di gestione e di pianificazione dei soprassuoli forestali, fino ai modelli di previsione della loro dinamica nel tempo (tavole alsometriche), espressione più matura dell’interesse economico per il bosco produttore di legno ([4]). Il passaggio da una gestione orientata alla produzione ad una gestione di tipo multifunzionale e sostenibile ([14], [3]) ha allargato l’attenzione alla stima della produttività biologica in termini di energia o di sostanza secca. La stima delle fitomasse rappresenta così la tappa recente di un approccio classico che, dalla determinazione e previsione del volume commerciabile, si è ampliato verso la determinazione della biomassa epigea considerata sia nel suo complesso e sia nelle sue componenti principali: massa del fusto, dei rami e massa fogliare ([27]).
La funzione emergente del bosco come sink di carbonio e la necessità di quantificarne gli stock ed il ritmo di accumulo rappresenta oggi una ragione ulteriore per una accurata determinazione della massa arborea come frazione importante dell’intero serbatoio suolo-soprassuolo ([11], [25], [21], [6], [16], [26], [8]).
Da quanto sopra riportato si evince come i lavori sulla stima della fitomassa arborea siano sempre stati di rilevante utilità per gli studi ecosistemici e stiano assumendo sempre maggiore importanza per le nuove esigenze dettate dagli impegni previsti dalla Convenzione sul clima e dal Protocollo di Kyoto ([34], [17]).
A causa degli elevati costi del rilievo diretto in campo della massa arborea, i metodi attualmente più utilizzati per questa determinazione sono le stime indirette e, tra queste, le equazioni di previsione sviluppate in modo da restituire valori di biomassa a partire da grandezze facilmente misurabili in campo, quali diametro e altezza della pianta ([31]).
Il principale problema dell’utilizzo delle equazioni di biomassa è la loro applicabilità limitata alle specie e alle condizioni locali della stazione su cui i modelli sono stati approntati; da qui gli sforzi nel produrre equazioni a scala più ampia ([18], [38], [37], [36]) e nel riunire le equazioni già esistenti in database esaustivi in modo da facilitare ed incrementare la diffusione di tali strumenti ([33], [19], [39]).
In questo contesto appare di rilevante interesse lo sviluppo di equazioni per la stima della fitomassa per specie e regioni che ne sono carenti e per tipi di bosco, come i cedui in evoluzione naturale ed in avviamento ad altofusto, che mancano assolutamente di modelli dendro-auxonomici di riferimento in quanto tipologie di “neoformazione”. Queste hanno avuto infatti diffusione crescente a partire dagli anni ’70 del secolo scorso, a seguito della sospensione delle utilizzazioni e dell’allungamento dei turni tradizionali nell’area originale del ceduo.
In Toscana, regione in cui i cedui di querce caducifoglie in generale e di cerro in particolare trovano la maggiore diffusione tra le regioni italiane, sono bene rappresentati sia tutti gli ambienti di vegetazione della specie, dalla zona sub-costiera a quella collinare interna fino all’area pre-appenninica ed appenninica, sia i tipi strutturali originati dalle diverse opzioni di gestione attuate.
Obiettivo, quindi, del presente lavoro è quello di produrre uno strumento di stima della fitomassa arborea epigea per i cedui in avviamento di cerro in Toscana. La disponibilità di numerosi siti installati e regolarmente monitorati dall’Istituto Sperimentale per la Selvicoltura di Arezzo fino dai primi anni ’70 e la necessità di produrre stime affidabili dei volumi e delle fitomasse presenti ai successivi inventari, hanno condotto alla raccolta periodica di campioni di alberi. Modelli di previsione a carattere locale sono stati realizzati in collaborazione con la sezione di Biometria forestale dell’Istituto Sperimentale per l’Assestamento Forestale e l’Alpicoltura di Trento (Ghetti & Fabbio, Fabbio & Tabacchi, dati non pubblicati) per valutazioni di carattere ecologico-funzionale specifiche ai siti sperimentali. Data la consistenza delle informazioni accumulate nel tempo si è ritenuto poi di riunire i singoli campioni per produrre strumenti estimativi a più ampia valenza territoriale, utilizzabili anche a scopo inventariale. Questo lavoro si collega quindi a una serie di contributi sulla stima dei volumi e delle fitomasse arboree epigee realizzati sulle stesse tipologie di bosco ([2]: faggio; [5], [13]: leccio; [1]: cerro) e su tipi differenti ([23], [24], [32], [7], [15]).
Questo contributo si collega in particolare a quello dedicato ai soprassuoli di cerro della Toscana centro-meridionale ([1]) in cui sono riportati diversi modelli estimativi del volume del fusto e della fitomassa arborea epigea. L’attuale set di dati integra i precedenti per le dimensioni degli alberi modello, pari a quelle massime osservabili oggi nella componente dominante dei cedui invecchiati e nella struttura delle fustaie da pollone.
Materiali e metodi
Descrizione dell’area di studio e dei siti di campionamento
Il campionamento è stato condotto in 4 siti che comprendono i principali ambienti di vegetazione del cerro in Toscana, dalla fascia collinare sub-costiera centro-meridionale fino alle aree pre-appenninica ed appenninica che si incontrano risalendo la regione verso nord-est. Il cerro trova infatti condizioni idonee di vegetazione in un ampio gradiente di quota e di variazioni termo-udometriche, utilizzando le combinazioni favorevoli di orografia ed esposizione.
Le caratteristiche stazionali ed i parametri del soprassuolo (densità e struttura) descrivono tipologie forestali relativamente omogenee. L’età dei soprassuoli di provenienza dei campioni, determinata dalla conta degli anelli annuali sulle sezioni radiali di base, è compresa tra 45 e 52 anni. Queste età corrispondono a quelle prevalenti nei primi avviamenti ad altofusto eseguiti. Le strutture, coetanee, hanno fisionomia di fustaia monoplana derivata dal taglio di avviamento del ceduo e da uno o due successivi diradamenti. La “filatura” dei polloni, che tendono a mantenere la posizione nel piano dominante per le caratteristiche di eliofilia della specie, determina una variazione di altezza ridotta pur in presenza di una struttura diametrica ancora differenziata. Già il primo diradamento (taglio di avviamento) modella la struttura originale del ceduo in una fisionomia di fustaia di età simile. Il solo elemento distintivo dell’origine del bosco è dato dalla permanenza di più di un pollone di pari sviluppo (in genere fino a due) su alcune ceppaie. Già il successivo diradamento risolve generalmente questa distribuzione ancora parzialmente raggruppata, che comunque non influisce sul dendrotipo a parità di classe sociale. L’impostazione e la struttura della chioma mantengono infatti la forma appressata tipica dei polloni fino alle età osservate.
I principali parametri dendrometrici e stazionali dei siti sono riportati in Tab. 1. Le densità prevalenti sono di 700-800 alberi ad ettaro tranne che per il sito 4, diradato due volte nel ciclo di avviamento; l’area basimetrica corrente è variabile da 27 a 31 m2 ha-1 con incremento medio annuo da 0.5 a 0.7 m2 ha-1, il diametro dominante è compreso tra 28 e 38 cm e l’altezza dominante tra 23 e 25 m. Tutti i parametri confermano la ridotta variazione di fertilità stazionale e di produttività di questi soprassuoli, già evidenziata per età precedenti e per il complesso dei siti monitorati e di estrazione di campioni di alberi modello in Toscana ([1]).
Tab. 1 - Siti di prelievo degli alberi modello (a.m.): parametri stazionali e dendrometrici. G: area basimetrica; Im: incremento medio; d: diametro; h: altezza.
| N | Sito | a.m. n° | Quota m | Esp. prev |
Coord. Geogr. |
Età anni |
Polloni n° ha-1 | Gcorr m2 ha-1 |
Im Gcorr m2 ha-1 |
dmedio cm | hmedio m |
ddom cm |
hdom m |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Fosso Cagnesi (Colline Metallifere) |
43 | 580 | NE | 43°11’N 10°51’E |
45 | 796 | 28.88 | 0.64 | 21.5 | 21.4 | 32.3 | 24.1 |
| 2 | Valsavignone (Alta Valtiberina) |
24 | 750 | NE | 43°30’N 12°03’E |
47 | 784 | 31.02 | 0.66 | 22.5 | 21.4 | 30.4 | 24.3 |
| 3 | Asqua (Foreste Casentinesi) |
15 | 790 | S | 43°46’N 11°52’E |
52 | 788 | 26.63 | 0.51 | 20.7 | 20.5 | 27.8 | 22.6 |
| 4 | Pian d’Acero (Alpe di Catenaia) |
32 | 915 | NO | 43°38’N 11°56’E |
45 | 419 | 29.78 | 0.66 | 30.1 | 24.6 | 38.2 | 25.2 |
| - | Media | - | - | - | - | 47 | 697 | 29.08 | 0.62 | 23.7 | 22.0 | 32.2 | 24.1 |
Il campionamento, le misure in campo e in laboratorio
L’insieme degli alberi modello include i dendrotipi e le classi dimensionali presenti nella struttura del soprassuolo. I campioni sono formati da soggetti abbattuti a seguito di diradamenti di tipo misto e da prelievi nelle aree circostanti i siti sperimentali. Gli alberi modello sono stati inclusi nel campione in base a caratteristiche comuni del dendrotipo quali: chioma di normale impostazione e sviluppo, fusti non biforcati e privi di anomalie di forma evidenti. La stratificazione preliminare del soprassuolo ha consentito di rappresentare ciascuna componente sociale secondo il peso relativo. Sono stati complessivamente considerati 113 alberi modello; in Tab. 2 è riportato il numero di osservazioni ripartito per classi di diametro e altezza.
Tab. 2 - Ripartizione degli alberi modello per classi di diametro e di altezza.
| Classi di diametro (cm) | Classi di altezza (m) | |||
|---|---|---|---|---|
| h < 18 | 18 ≤ h < 21 | h > 21 | Totale | |
| d < 17.5 | 12 | 13 | 1 | 26 |
| 17.5 ≤ d < 22.5 | 6 | 23 | 26 | 55 |
| 22.5 ≤ d < 27.5 | - | 10 | 14 | 24 |
| d ≥ 27.5 | 1 | 2 | 5 | 8 |
| totale | 19 | 48 | 46 | 113 |
All’abbattimento il protocollo di rilievo ha previsto per ciascun albero modello: (i) la misurazione delle circonferenze sopra corteccia del fusto a 1.30 m e ad intervalli di 1 m dalla sezione a 0.5 m dal suolo fino al diametro di svettamento di 3 cm; (ii) la misurazione dell’altezza totale; (iii) la separazione, raccolta e pesatura delle diverse frazioni della chioma: rami grossi (> 3 cm) e rami sottili (cimale compreso); (iv) il prelievo di porzioni di fusto e rami per le successive determinazioni di laboratorio. La massa fogliare è sempre esclusa dato che gli abbattimenti sono stati effettuati nel periodo invernale.
In laboratorio sono stati determinati: (i) il rapporto ponderale (peso secco/peso fresco), (ii) la massa volumica (peso fresco/volume) e (iii) la densità basale (peso secco/volume), per le porzioni di fusto prelevate in campo; il rapporto ponderale per i campioni di rami grossi e sottili. Il volume delle porzioni di fusto è stato determinato per immersione; il peso secco in stufa ventilata a 95°C per pesate successive fino a peso costante. Il volume del fusto svettato è stato calcolato per via geometrica applicando la formula della sezione mediana.
Con le misure di campo e le determinazioni di laboratorio, infine, sono stati calcolati il peso secco di ciascuna componente arborea (fusto, rami grossi, rami sottili) e il peso secco totale epigeo per albero modello.
Nel caso del sito 4, Pian d’Acero, il rapporto ponderale (peso secco / peso fresco) è stato calcolato unitamente per le due componenti di rami (vedi Tab. 3); ai fini della modellizzazione il calcolo del peso secco delle due componenti rami grossi e rami sottili (pesate separatamente in campo) è stato effettuato utilizzando i rapporti ponderali ottenuti negli altri siti.
Tab. 3 - Statistiche delle determinazioni di laboratorio. sd: deviazione standard; cv: coefficiente di variazione. (°) Rami grossi >3 cm; rami sottili ≤ 3 cm.
| Sito | Parametro | Rapporto ponderale (peso secco/peso fresco) |
Massa volumica (peso fresco/volume) g/cm3 |
Densità basale (peso secco/volume) g/cm3 |
||
|---|---|---|---|---|---|---|
| fusto | rami grossi (°) |
rami sottili (°) |
fusto | fusto | ||
| Fosso dei Cagnesi (1) |
media | 0.62 | 0.66 | 0.67 | 1.17 | 0.72 |
| sd | 0.01 | 0.02 | 0.14 | 0.18 | 0.11 | |
| cv (%) | 2.1 | 3.7 | 20.9 | 15.3 | 14.9 | |
| Valsavignone (2) |
media | 0.62 | 0.63 | 0.66 | 1.09 | 0.68 |
| sd | 0.01 | 0.02 | 0.06 | 0.03 | 0.02 | |
| cv (%) | 2.4 | 3.5 | 8.4 | 2.5 | 3.4 | |
| Asqua (3) |
media | 0.60 | 0.62 | 0.61 | 1.07 | 0.55 |
| sd | 0.12 | 0.02 | 0.01 | 0.02 | 0.25 | |
| cv (%) | 19.5 | 3.3 | 2.2 | 1.4 | 44.6 | |
| Pian d’Acero (4) |
media | 0.62 | 0.59 | - | 1.07 | 0.66 |
| sd | 0.05 | 0.02 | - | 0.06 | 0.03 | |
| cv (%) | 8.5 | 2.8 | - | 5.9 | 4.3 | |
I modelli di previsione
Per l’approntamento delle equazioni di previsione del volume e della fitomassa arborea, è stata impiegata l’analisi di regressione nella variante dei minimi quadrati ponderati.
Sono state studiate cinque equazioni, una per la stima del volume del fusto (V) e le restanti quattro per le componenti di fitomassa e per la fitomassa epigea totale. Le variabili dipendenti per la fitomassa sono state così distinte: peso secco del fusto (w1); peso secco dei rami grossi (w2); peso secco dei rami sottili (w3) e peso secco totale epigeo (wtot). Attraverso le equazioni di previsione, le variabili da stimare vengono così espresse in funzione di grandezze (diametro a 1.30 m e altezza totale) facilmente misurabili in campo e oggetto di normale rilievo dendrometrico. La scelta delle variabili indipendenti è stata effettuata cercando il miglior compromesso tra semplicità del modello e suo adattamento ai dati reali. Il prodotto del quadrato del diametro (d) e dell’altezza totale (h) della pianta è stato impiegato come variabile predittiva principale, in quanto variabile che esprime in modo compatto le dimensioni dell’albero. A questa è stata aggiunta una seconda variabile scelta tra le possibili combinazioni del prodotto di d e h elevate alle potenze 0, 1 o 2, in modo da massimizzare la varianza spiegata dal modello.
La scelta del modello è stata effettuata analizzando i dati di volume del fusto, nell’ambito della tecnica di regressione lineare multipla univariata, ricercando l’equazione di perequazione con una distribuzione ottimale delle differenze tra valori attesi e valori sperimentali. Tale modello è stato poi utilizzato anche per lo sviluppo delle equazioni di fitomassa, calibrate con la tecnica della regressione lineare multipla multivariata in modo da garantire l’additività delle stime delle equazioni per le singole componenti rispetto al corrispondente valore previsto dall’equazione di stima della fitomassa totale.
Per superare, infine, il problema della non omogeneità della varianza delle variabili dipendenti, sempre presente nel caso del volume e della fitomassa arborea, è stata impiegata una funzione di ponderazione che lega la variabilità delle singole variabili dipendenti alle dimensioni degli alberi, con forma vari= (di2 hi)k, ponendo il coefficiente k sempre pari a 2, secondo una semplificazione ormai ampiamente accettata ([22], [35]).
La metodologia qui sinteticamente richiamata per l’approntamento dei modelli previsionali è illustrata in dettaglio nel lavoro di Fattorini et al. ([15]), al quale si rimanda per eventuali approfondimenti.
Risultati
Nella Tab. 3 sono riassunte le statistiche descrittive delle principali determinazioni di laboratorio sui campioni arborei. La Tab. 4 riporta i valori minimo, medio e massimo delle variabili prese in esame nell’analisi di regressione. Nella Tab. 5 sono riportati il modello generale adottato, i coefficienti delle cinque equazioni sviluppate, i relativi valori del coefficiente di determinazione e dell’errore standard calcolati sui valori ponderati e non, questi ultimi particolarmente utili nel caso di confronti tra modelli differenti. Viene anche presentato il coefficiente di variazione percentuale della stima sui valori non ponderati ([29], [9], [28]).
Tab. 4 - Statistiche descrittive per alcune grandezze relative agli alberi modello. d: diametro del fusto a 1.30 m dal suolo; h: altezza totale; V: volume del fusto; w1: peso secco del fusto; w2: peso secco dei rami grossi; w3: peso secco rami sottili; wtot: peso secco totale epigeo.
| Parametro | Min | Media | Max |
|---|---|---|---|
| d (cm) | 10.8 | 20.5 | 30.9 |
| h (m) | 14.2 | 20.3 | 28.5 |
| V (dm3) | 65.5 | 336.6 | 739.5 |
| w1 (kg) | 43.1 | 230.5 | 486.1 |
| w2 (kg) | 0.0 | 10.7 | 64.2 |
| w3 (kg) | 0.3 | 13.7 | 61.5 |
| wtot (kg) | 44.4 | 254.6 | 570.9 |
Tab. 5 - Statistiche delle equazioni di previsione del volume e di tutte le componenti di biomassa (per la simbologia cfr. Tab. 4). Sono riportati i coefficienti delle equazioni (bi), il numero di osservazioni su cui sono stati calibrati i modelli (n), il coefficiente di determinazione (R2 adj), l’errore standard (SE), il coefficiente di variazione percentuale dell’equazione (CV). (a): Valori calcolati sulle variabili non ponderate.
| Modello: y = b 1 +b 2 d 2 h+b 3 d | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Variabili dipendenti |
Statistiche | ||||||||
| b1 | b2 | b3 | n | R2 adj | SE | R2 adj(a) | SE(a) | CV%(a) | |
| V | -72.05464 | 0.02642 | 8.31076 | 113 | 0.991 | 3.649 10-3 | 0.941 | 35.522 | 10.5 |
| w1 | -74.21837 | 0.01597 | 7.87599 | 113 | 0.986 | 3.154 10-3 | 0.912 | 29.817 | 12.9 |
| w2 | -15.60991 | 0.000132 | 1.20792 | 113 | 0.672 | 7.885 10-4 | 0.481 | 8.081 | 78.5 |
| w3 | -7.18356 | 0.00097 | 0.58573 | 113 | 0.873 | 5.701 10-4 | 0.600 | 6.016 | 44.3 |
| wtot | -97.01184 | 0.01703 | 9.66964 | 113 | 0.985 | 3.566 10-3 | 0.918 | 32.716 | 12.8 |
La presenza di variabili indipendenti tra loro correlate ha reso necessario il controllo del fenomeno della multicollinearità ([10], [28]) tramite il calcolo dei fattori di inflazione della varianza (VIF) e l’impiego delle tecnica della ridge regression ([30]). Il fenomeno si è dimostrato per i dati qui presentati trascurabile.
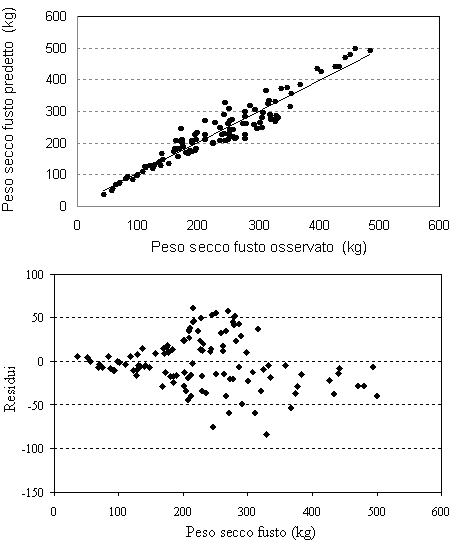
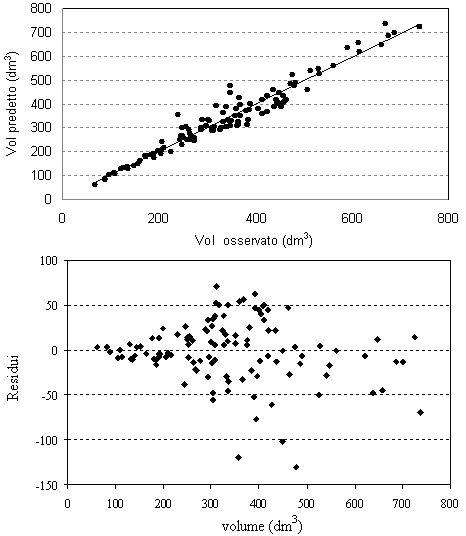
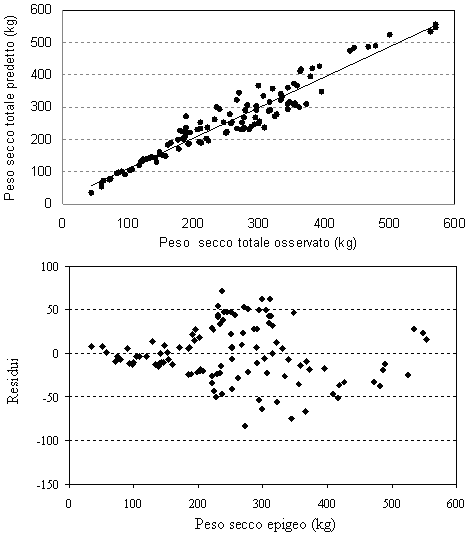
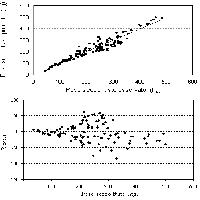
Nelle figure 1-5 (Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5) sono presentate le distribuzioni dei valori misurati in funzione dei valori stimati e le distribuzioni dei residui per tutte le equazioni di previsione. La media dei residui con segno è risultata pari a -1.14 dm3 per il volume del fusto, a -0.95 kg per il peso secco del fusto, a 0.42 kg per il peso secco dei rami grossi, a 0.14 kg per il peso secco dei rami sottili e a -0.38 kg per il peso secco totale epigeo.
Fig. 2 - Valori predetti vs. valori osservati e distribuzione dei residui per il peso secco del fusto.
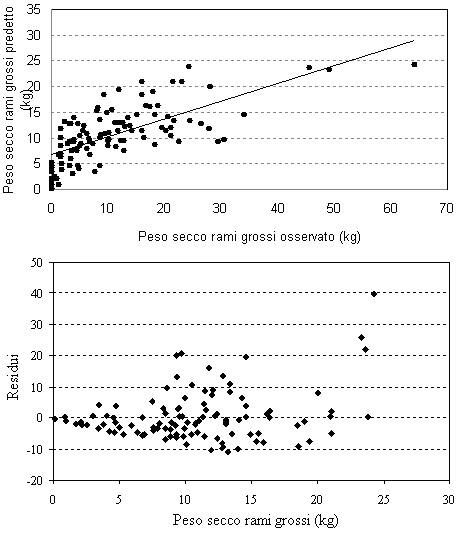
Fig. 3 - Valori predetti vs. valori osservati e distribuzione dei residui per il peso secco dei rami grossi.
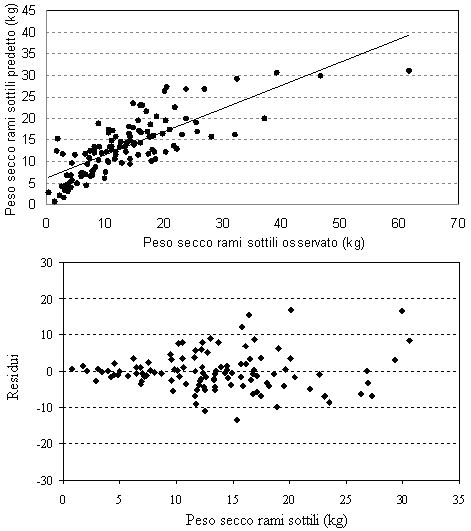
Fig. 4 - Valori predetti vs. valori osservati e distribuzione dei residui per il peso secco dei rami sottili.
Fig. 5 - Valori predetti vs. valori osservati e distribuzione dei residui per il peso secco totale epigeo.
Discussione e conclusioni
Le statistiche riportate per descrivere il campione e le equazioni qui approntate (Tab. 4, Tab. 5), utili nel momento in cui si disponga di dati dendrometrici da utilizzare per il calcolo della fitomassa e si debba quindi scegliere un modello idoneo per farlo ([9], [28]), depongono per una buona precisione di stima delle variabili dipendenti. In particolare, i valori più alti del coefficiente di determinazione si ottengono per l’equazione relativa al volume del fusto, grandezza su cui è stata fatta la scelta del modello, e per le equazioni del peso secco del fusto e della fitomassa epigea totale. Le altre componenti della fitomassa, rami grossi e rami sottili, presentano valori di R2 minori ed errori standard maggiori, se comparati con la dimensione media della variabile predetta (Tab. 5). Questo può essere spiegato dalla maggiore variabilità dei dati grezzi su cui è stato tarato il modello per queste componenti, ma anche dalla generale difficoltà nel predire tramite equazioni le componenti della chioma, soprattutto per le latifoglie ([20]).
Introdurre nel modello una variabile aggiuntiva che tenesse conto della posizione nella struttura verticale della singola pianta (dominata, codominante o dominante) avrebbe sicuramente portato a un migliore adattamento del modello ai dati reali, ma due considerazioni devono essere qui riportate: in primo luogo la stratificazione dei popolamenti in esame è ridotta e, ancora più importante, lo scopo principale del lavoro è quello di fornire strumenti utilizzabili nella prassi. Inserire un maggior numero di variabili indipendenti significa dover avere maggiori informazioni al momento dell’applicazione del modello, situazione che non sempre si verifica in particolar modo nel caso di rilievi inventariali ([10], [15]). Tutti i fattori di variazione non compresi nelle variabili esplicative sono considerati nella componente di errore, per cui il modello risultante sarà sicuramente meno preciso nella determinazione dei valori attesi ma più pratico e di più ampia applicabilità. Il trade-off tra adattamento e semplicità del modello è una questione tuttora irrisolta.
I grafici che rappresentano l’andamento dei residui ed i valori predetti in funzione di quelli osservati (Fig. 1 - Fig. 5) mostrano una leggera sovrastima delle equazioni del volume e del peso secco del fusto per le classi diametriche maggiori. Le classi dimensionali superiori sono quelle che, infatti, presentano la maggiore variabilità delle grandezze da stimare e per le quali si dovrebbe quindi avere un più elevato numero di osservazioni campionarie. Questo non è spesso proponibile a causa dell’onerosità dei costi delle misurazioni in campo e soprattutto per gli alberi di grandi dimensioni.
Come già precedentemente segnalato, anche dai grafici relativi all’equazione di previsione del peso secco dei rami grossi (Fig. 3) si riscontrano problemi per questa componente, soprattutto nelle stime per le classi diametriche inferiori. Limitatamente a questa componente di fitomassa si sono riscontrati dei valori negativi nelle classi ipso-diametriche al limite inferiore del campo esplorato. In tale situazione si consideri il valore negativo come nullo e si sommino solo i valori componenti positivi, ricalcolando così il valore totale per la determinazione della fitomassa epigea totale.
È utile ribadire l’opportunità del controllo preventivo di compatibilità dei dati grezzi su cui è stato calibrato il modello prima di applicare equazioni di previsione su dati dendrometrici provenienti da un determinato sito o regione ([9], [28]). In particolare, sono da verificare le dimensioni massime e minime degli alberi modello utilizzati, la tipologia di soprassuolo, i parametri dendrometrici di riferimento e le caratteristiche stazionali (fertilità). Le equazioni di previsione sono state calcolate su popolamenti relativamente omogenei e possono essere utilizzate per la stima del volume e della biomassa in situazioni comparabili a quelle qui presentate.
Sono attualmente allo studio modelli più generali ([18], [38], [36]) che possono essere applicati a scala maggiore, ma si deve sempre tener presente il giusto compromesso tra applicabilità ed errore della stima e valutare in ogni situazione l’effettiva possibilità di utilizzo delle equazioni esistenti. Rimane il fatto che, quando disponibili, le equazioni di previsione sono considerate lo strumento da preferire per stimare la fitomassa arborea partendo da dati inventariali correnti ([31]).
Nel caso in esame, la progressiva applicazione del trattamento (diradamenti) tende, già alle età qui considerate, a ridurre la variabilità dendrometrica iniziale ed a far convergere la struttura dei soprassuoli verso un modello comune ([12]). Ciò, insieme alla ridotta variazione di fertilità tra i siti, fa presupporre un’applicabilità ampia del modello elaborato fino a quando la variazione del dendrotipo arboreo, soprattutto a livello di chioma, non segnalerà la necessità di provvedere a ulteriori campionamenti e all’elaborazione di nuove funzioni di stima.
La diffusione nell’Italia centrale di tipologie di soprassuolo simili a quelle analizzate evidenzia l’utilità degli strumenti elaborati.
Ringraziamenti
La ricerca è stata condotta nell’ambito dei progetti Riselvitalia Area 3 “Selvicoltura e sostenibilità”, Progetto 3.2: “Selvicoltura, funzionalità e gestione sostenibile dei cedui nell’area appenninica e mediterranea” finanziato dal MiPAF e "Selvicoltura sostenibile nei boschi cedui" finanziato da Arsia-Regione Toscana. Il lavoro è stato svolto in parti uguali dagli autori.
References
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar