Spatialization of climatic data at the Italian national level by local regressive models
Forest@ - Journal of Silviculture and Forest Ecology, Volume 4, Pages 213-219 (2007)
doi: https://doi.org/10.3832/efor0453-0040213
Published: Jun 19, 2007 - Copyright © 2007 SISEF
Research Articles
Abstract
The availability of spatialised climatic data is an essential pre-requisite for the implementation of GIS-based analysis in many application fields. Among the different methodologies for the spatialization of climatic data collected in weather-stations the most used are those based on geostatistical approaches, on parametric correlative models or on neural networks. Within the “Completamento delle Conoscenze Naturalistiche di Base” project, funded by the Italian Ministry for the Environment (Department of Nature Protection) a database of 403 weather-stations distributed across Italy with a time series of thirty years was collected. Data of mean monthly temperature (minimum and maximum) and rainfalls were spatialized by a local linear univariate regressive method based on elevation as independent variable. A total of 36 monthly maps with a geometric resolution of 250 m was generated. The present paper introduces the adopted methodology and the accuracy results estimated by leave-one-out cross validation.
Keywords
Climate, Meteorological data, Spatialization, Regressive models, Italy
Introduzione
La pianificazione delle risorse territoriali e ambientali necessita, per una corretta impostazione delle più idonee opzioni gestionali, di una rilevante mole di dati georeferenziati che al contempo abbiano elevata qualità, sia tematica che geometrica, e sufficiente livello di omogeneità rispetto agli standard di riferimento esistenti.
L’influenza dei fattori climatici sulla diffusione dei diversi biomi terrestri è fenomeno noto in ecologia, alle diverse scale di riferimento. Nel tempo sono stati proposti vari tentativi di classificazione al fine di inquadrare sistematicamente e di individuare l’estensione geografica dei diversi climi. Con specifico riferimento allo studio delle relazioni tra clima e vegetazione i sistemi di classificazione maggiormente utilizzati sono su base “causale”. In questa categoria rientrano anche le classificazioni fitoclimatiche ([15], [5], [16], [2]), che distinguono le diverse classi in funzione, prevalentemente, di valori soglia di temperature e precipitazioni o di indici da essi derivati.
Le operazioni di raccolta e standardizzazione di dati utili per la derivazione di informazioni climatiche sono tanto più onerose quanto più dettagliata vuole essere la rappresentazione della variabilità del fenomeno a livello geografico.
La possibilità di spazializzare i dati meteo-climatici acquisiti puntualmente sul territorio per derivarne mappe tematiche permette di ottenere un’immagine sinottica del fenomeno sul territorio stesso. Per questo motivo tali strati informativi risultano particolarmente apprezzati nei più diversi settori applicativi della pianificazione ambientale.
In letteratura sono reperibili molteplici procedure che permettono di inferire a intere superfici valori meteoclimatici puntuali quali, appunto, la temperatura e la precipitazione acquisite da stazioni meteorologiche ([10], [19]). Da citare sono i metodi stocastici afferenti al settore della geostatistica come kriging e cokriging ([14]) e quelli basati sull’uso di reti neurali ([8]).
Nel presente lavoro viene presentata una procedura innovativa per la spazializzazione di variabili climatiche a livello nazionale, basata sull’utilizzo del metodo della regressione lineare pesata localmente ([4]).
La base di dati
L’area di indagine interessa tutto il territorio italiano e si estende tra 36° e 47° 30’di latitudine nord e tra 5° 30’e 18° 30’di longitudine est.
La quota s.l.m., parametro che la metodologia adotta come variabile indipendente nel metodo regressivo, fa riferimento a un modello digitale del terreno dell’Italia con pixel di 250 m ottenuto per ricampionamento di un DEM (Digital Elevation Model) con passo originario di 75 m. Il sistema di proiezione considerato è UTM fuso 32 nord su datum WGS84.
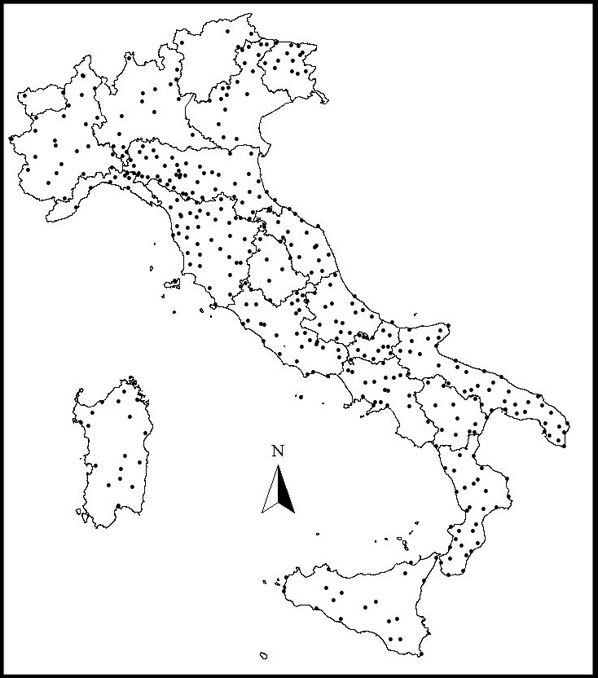
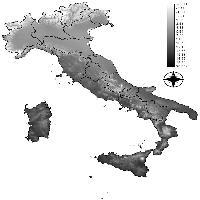
La base dati meteorologica è costituita da misurazioni giornaliere relative a temperature minime, massime e precipitazioni acquisite per un periodo di circa trenta anni (periodo 1950-1980) in 403 stazioni termopluviometriche dislocate sul territorio nazionale (Fig. 1). La base di dati è stata acquisita nell’ambito del progetto “Completamento delle Conoscenze Naturalistiche di base” (Unità di Ricerca del Dipartimento di Biologia Vegetale dell’Università“La Sapienza” e Istituto di Ecologia ed Idrologia Forestale del Consiglio Nazionale delle Ricerche di Cosenza, responsabili scientifici C. Blasi e F. Iovino - [3]). L’elaborazione dei dati grezzi ha permesso di colmare i dati mancanti con una procedura di gap filling basata sulla correlazione locale tra stazioni meteo vicine ([7]) e quindi di calcolare per ogni stazione i valori climatici medi mensili riferiti alle tre variabili osservate. I dati aggregati mensili sono stati calcolati nel seguente modo: la temperatura media massima mensile come media dei massimi giornalieri; la temperatura media minima mensile come media dei minimi giornalieri; le precipitazioni mensili come somma delle precipitazioni giornaliere; i dati mensili sono stati quindi mediati lungo tutto il periodo trentennale della serie temporale disponibile.
Metodo di spazializzazione
Il sistema di spazializzazione proposto trova il proprio fondamento sulla calibrazione a livello locale (cioè pixel per pixel) dei parametri di una regressione lineare (medie e matrici di varianza e covarianza) tra le diverse variabili dipendenti (temperature medie minima e massima, precipitazioni mensili) con la variabile indipendente quota estratta dal modello digitale del terreno. A ogni pixel dell’immagine corrisponde quindi una propria specifica equazione che predice la variabile dipendente in funzione della quota.
L’applicazione di procedure di regressione uni- o multivariata su superfici relativamente ampie per la spazializzazione di attributi meteo-climatici è fondata sull’assunto di omogeneità che prevede la sostanziale costanza della relazione che lega la variabile dipendente oggetto della spazializzazione con le variabili indipendenti considerate ([1]). Tale assunto trova evidenti limiti applicativi sul territorio italiano a causa dell’accentuata eterogeneità spaziale del fenomeno qui indagato ([9], [13]). Per questi motivi le procedure calibrate localmente permettono di aumentare significativamente l’accuratezza e l’affidabilità statistica delle procedure di spazializzazione ([12]).
I modelli di regressione localmente calibrata si fondano sullo stesso principio dei metodi stocastici geostatistici come kriging e cokriging ([4], [20]): “le cose tra loro più vicine sono più simili rispetto alle cose tra loro più lontane ” (prima legge della geografia di Tobler).
Tradizionalmente le procedure di regressione lineare multivariata descrivono l’interrelazione tra la variabile dipendente e una o più variabili indipendenti determinando i vettori della media e delle matrici di varianza/covarianza ([1]). Questi parametri derivano dall’analisi di un set di training nei quali sia il valore della variabile dipendente che di quella/e indipendente/i sono noti.
Il modello per la spazializzazione qui proposto prende spunto dalla teoria del fuzzy set ([21]) secondo la quale le equazioni di regressione possono essere ottenute assegnando un peso ad ogni elemento del set di training ([17], [18]).
In particolare, la media fuzzy (Meani*) di ogni i-esima variabile (dipendente o indipendente), può essere quantificata nel seguente modo (eqn. 1):
dove le sommatorie vengono applicate per ogni elemento del campione, Vxi è il valore della variabile per l’elemento campionario x, mentre Wx è il peso dato all’elemento campionario. Analogamente, ogni elemento delle matrici di varianza/covarianza fuzzy (Covij ) può essere trovato come segue ([17], [18] - eqn. 2):
Da un punto di vista operativo per ciascun pixel per il quale debba essere stimato il valore ignoto della variabile dipendente climatica viene calcolato un modello di regressione lineare univariata usando, di tutto il set di training costituito dalle informazioni acquisite nelle 403 stazioni meteorologiche disponibili, preferenzialmente quelle più vicine al pixel in esame ([11]).
I dati delle stazioni localmente più vicine vengono pesate sulla base di una relazione esponenziale negativa rispetto alla distanza euclidea (eqn. 3):
dove Wx è il peso fuzzy assegnato a ciascun pixel di training x; Dx è la distanza euclidea (distanza orizzontale espressa in km) fra il pixel in esame e la stazione considerata; R è il range della funzione (distanza orizzontale, espressa nella stessa unità di misura di Dx ) che permette all’operatore di definire l’importanza relativa delle stazioni più vicine al pixel incognito rispetto a quelle più lontane ([11]). Al diminuire del valore diR aumenta il peso assegnato alle stazioni più vicine rispetto a quelle più lontane: per valori di R molto grandi il peso delle stazioni è quasi uguale, indipendentemente dalla loro distanza dal pixel in esame.
La scelta del valore di range (R) più appropriato è essenziale perché esso determina le stazioni che vengono maggiormente considerate nella stima diMeani*: in altre parole vengono considerate localmente solo le stazioni che si trovano entro una distanza pari o inferiore aR.
Nella sperimentazione il valore ottimale di R è stato determinando verificando l’accuratezza dei risultati tramite leave-one-out cross validation ([6]). Questo metodo consiste nell’escludere un punto di riferimento dalla costruzione di un modello di stima, che è poi applicato proprio sul punto escluso. La ripetizione di tale processo per tutti i punti di riferimento (le 403 stazioni termopluviometriche) consente di ottenere una serie completa di stime che possono poi essere confrontate con i dati misurati. Nel caso specifico la procedura è stata applicata con diversi valori di R delle regressioni localizzate, fino ad individuare quello che mediamente produceva il minor errore.
Una volta quantificato R si è passati alla stima delle variabili climatiche per tutti i pixel dell’immagine. Sono state quindi generate 12 immagini mensili per ognuna delle tre variabili climatiche considerate
Risultati
Nel caso di studio il valore ottimale di R per il territorio italiano è risultato pari a 20 km. L’accuratezza della spazializzazione delle 36 variabili climatiche valutata tramite leave-one-out cross validation sulla base delle 403 stazioni meteorologiche utilizzate è presentata in Tab. 1. I risultati della spazializzazione delle minime mensili variano, in termini di accuratezza espressa come errore quadratico medio, tra 1.51 e 1.89 °C per le temperature massime, tra 1.49 e 1.84 °C per le minime e tra 14.2 e 66.4 mm per le precipitazioni.
Tab. 1 - Valori mensili del coefficiente di correlazione di Pearson (r) e dell’errore medio della stima in termini assoluti (BIAS, media dei valori stimati - media dei valori veri) e percentuali (BIAS% calcolato come BIAS rispetto alla media dei valori veri) ottenuti nella validazione con metodo leave-one-out della spazializzazione dei dati climatici considerati. I valori di BIAS per le temperature sono in gradi centigradi, quelli per le precipitazioni in mm.
| Mese | Precipitazioni | Temperature minime | Temperature massime | ||||||
|---|---|---|---|---|---|---|---|---|---|
| r | BIAS | BIAS% | r | BIAS | BIAS% | r | BIAS | BIAS% | |
| Gennaio | 0.64 | -0.42 | -0.30 | 0.91 | -0.06 | -4.73 | 0.92 | -0.03 | -0.42 |
| Febbraio | 0.65 | -0.34 | -0.29 | 0.91 | -0.05 | -2.71 | 0.90 | -0.02 | -0.23 |
| Marzo | 0.77 | -0.07 | -0.07 | 0.88 | -0.05 | -1.29 | 0.87 | -0.01 | -0.11 |
| Aprile | 0.82 | 0.25 | 0.30 | 0.86 | -0.05 | -0.74 | 0.83 | 0.00 | 0.02 |
| Maggio | 0.86 | 0.45 | 0.59 | 0.84 | -0.04 | -0.35 | 0.82 | 0.02 | 0.10 |
| Giugno | 0.91 | 0.42 | 0.69 | 0.85 | -0.04 | -0.25 | 0.82 | 0.04 | 0.14 |
| Luglio | 0.92 | 0.24 | 0.56 | 0.82 | -0.05 | -0.31 | 0.81 | 0.03 | 0.09 |
| Agosto | 0.90 | 0.12 | 0.21 | 0.85 | -0.05 | -0.27 | 0.83 | 0.01 | 0.05 |
| Settembre | 0.78 | 0.12 | 0.16 | 0.87 | -0.04 | -0.31 | 0.86 | 0.02 | 0.07 |
| Ottobre | 0.78 | -0.04 | -0.03 | 0.89 | -0.04 | -0.42 | 0.88 | -0.01 | -0.05 |
| Novembre | 0.78 | 0.08 | 0.05 | 0.91 | -0.04 | -0.66 | 0.91 | -0.03 | -0.20 |
| Dicembre | 0.73 | -0.04 | -0.03 | 0.92 | -0.04 | -1.58 | 0.92 | -0.04 | -0.39 |
Nell’arco dell’anno, gli errori di stima delle temperature massime tendono ad aumentare nel periodo estivo (giugno-agosto). Le temperature minime presentano una distribuzione dell’errore più omogenea e costante, pur presentando un picco nei mesi di luglio-agosto. Per le precipitazioni, invece, esiste un trend che vede i valori massimi di errore nei mesi invernali (dicembre-febbraio). Distribuzioni di questo tipo sono probabilmente dovute all’accentuata variabilità spaziale propria delle variabili climatiche.
Per quanto invece riguarda la distribuzione geografica, i valori massimi di errore si hanno, per tutte le tre variabili considerate, nelle zone più elevate. La presenza di errori maggiori nelle zone montuose è spiegabile considerando come forti dislivelli di quota creino gradienti significativi nelle variabili meteorologiche, che non sempre possono essere accuratamente modellizzati tramite procedure di spazializzazione statistica quali quella applicata. Anche l’effetto latitudinale sugli errori è probabilmente attribuibile alla presenza di montagne più alte nel Nord Italia.
Conclusioni
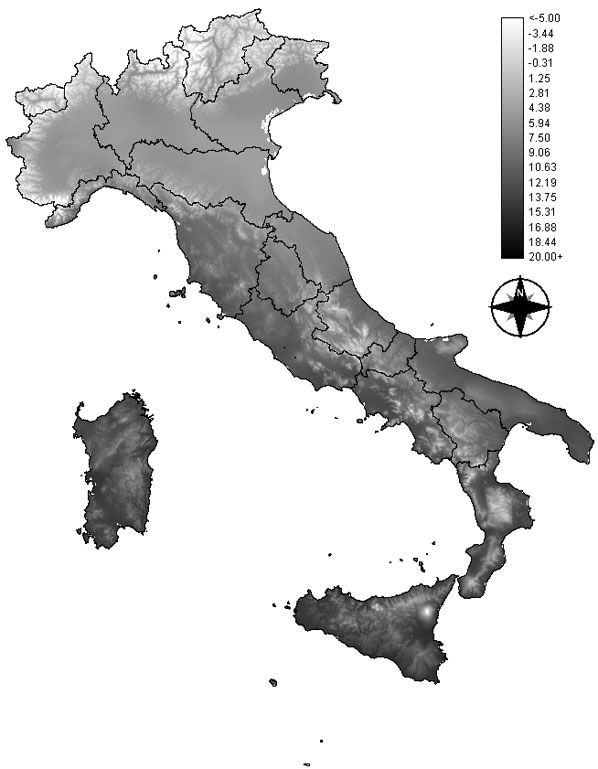
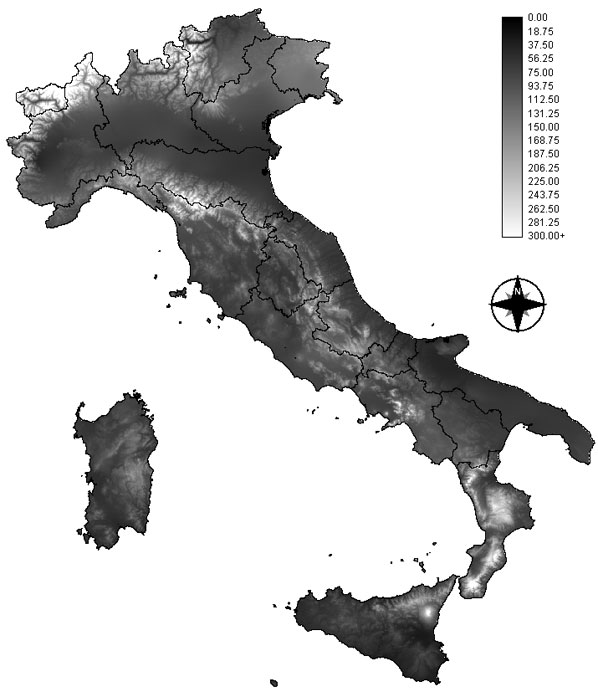
Seguendo l’approccio della regressione lineare univariata calibrata a livello locale la spazializzazione di un database meteoclimatico contenente i valori mediati su una serie temporale di trenta anni riferiti alle temperature minime, a quelle massime e alle precipitazioni mensili ha permesso di realizzare 36 strati informativi raster di 250 m di risoluzione geometrica. Immagini di esempio del risultato del processo di spazializzazione sono riportate nelle Fig. 2 e Fig. 3.
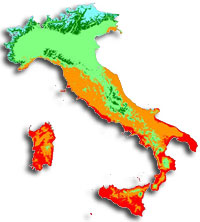
Fig. 2 - Risultato della spazializzazione dei dati delle temperature massime nel mese di gennaio (valori in °C).
Fig. 3 - Risultato della spazializzazione dei dati delle precipitazioni nel mese di marzo (valori in mm).
La scelta della quota come unica variabile indipendente determina una opportuna semplicità dei modelli generati, permettendo di ottenere risultati robusti sotto il profilo statistico e soddisfacenti in termini di accuratezza delle stime, anche in confronto a risultati analoghi ottenuti con tecniche di kriging e cokriging ([10]). In questo senso, l’efficacia applicativa del modello ha permesso di generare strati informativi di accuratezza e risoluzione geometrica tale da poter essere impiegati operativamente in applicazioni a supporto della pianificazione territoriale e ambientale.
References
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar