Production of climatic and bioclimatic maps by Universal Kriging with external drift: theory and examples for Italy
Forest@ - Journal of Silviculture and Forest Ecology, Volume 5, Pages 8-19 (2008)
doi: https://doi.org/10.3832/efor0507-0050008
Published: Mar 26, 2008 - Copyright © 2008 SISEF
Research Articles
Abstract
In this paper GIS-based maps of climatic and bioclimatic data for Italy have been obtained by interpolating values observed at measurement stations. Long-term (1961-1990) average monthly data were obtained from weather stations measuring precipitation (1102 sites) and temperature (321 sites). We analysed twelve climatic variables (temperature and precipitation) and nine bioclimatic indexes. Terrain variables and geographical location have been used as predictors of climate variables: longitude, latitude, elevation, aspect, slope, continentality and estimated solar radiation. Universal kriging (i.e., simple kriging with trend function defined on the basis of a set of covariates), which is optimal (i.e., BLUP, best linear unbiased predictor) if spatial association is present, has been used as spatial interpolator. Based on the root mean square errors from cross-validation tests, we ranked the best search radius for each variable data set. A 15 km search radius has been demonstrated to be the best one to model precipitation variables and precipitation-based bioclimatic indexes, while temperature variables were modelled using a 30 km radius.
Keywords
Bioclimatic indexes, GIS, Italy, Spatial interpolation, Universal kriging
Introduzione
Definire la nicchia bioclimatica rappresenta uno dei metodi più utilizzati per studiare e analizzare la distribuzione potenziale di una specie ([8], [41], [44], [23], [9] [16], [18], [39]) e gli effetti che eventuali cambiamenti climatici possono avere su tale specie e sulla sua distribuzione ([10], [24], [11], [18], [25], [5], [6], [35], [34]).
In passato molti Autori hanno utilizzato ed elaborato indici bioclimatici per interpretare le correlazioni tra variabili climatiche e distribuzione delle specie. Sulla base di tali indici si è arrivati ad alcune classificazioni bioclimatiche con la suddivisione del pianeta per macro-aree ([26], [4], [38]).
Generalmente il dato climatico di partenza di cui si dispone è un dato di tipo puntuale, proveniente dalla rete di stazioni termo-pluviometriche distribuite sul territorio. Per ottenere una carta che descriva l’andamento delle variabili su una superficie è necessario interpolare tale dato con tutti gli altri dati puntuali che si hanno a disposizione generando cosi superfici climatiche statistiche.
I metodi di interpolazione vengono utilizzati per stimare andamenti di temperatura e precipitazioni tenendo conto della distanza reciproca tra il punto geografico effettivamente misurato e quello da stimare (distance weighting - [40], [28], [43], [32], [27]). Altri metodi geostatistici universalmente riconosciuti come buoni predittori sono l’interpolazione polinomiale ([40], [28]), la regressione multipla e polinomiale ([17], [27], [1], [33], [7]), il kriging e le sue possibili modulazioni (ordinario, universale), co-kriging ([40], [36], [21], [20], [32], [14]), lo splines ([22], [28], [27]) e le reti neurali ([2]).
La scelta di utilizzare per questo lavoro l’Universal Kriging (UK) come metodo di interpolazione geostatistica è basata sulla considerazione che UK è riconosciuto essere uno dei migliori interpolatori per questo tipo di analisi e per questo tipo di dati, come emerso in uno studio comparativo con altri metodi comunemente utilizzati ([3]). Recentemente alcuni Autori ([7]) hanno prodotto mappe climatiche per il territorio italiano mediante applicazione di modelli regressivi localizzati utilizzando l’altitudine come unica variabile indipendente. Pur non esistendo alcuna prova che lo stimatore kriging sia migliore globalmente rispetto ad altre metodologie di stima, sappiamo che è stato dimostrato essere il best linear unbiased predictor (BLUP) e quindi ha caratteristiche di ottimalità accertate tra le procedure lineari. In letteratura infatti esistono esempi della maggiore efficienza del kriging rispetto alle regressioni locali ([30], [29], [19]). Tuttavia è anche vero che la scelta del variogramma può essere a volte cruciale e che metodi di interpolazione locale possono essere più flessibili rispetto al kriging dal momento che non necessitano di adattarsi ad un determinato variogramma.
Area di studio e dati climatici
L’area di studio ha interessato l’intero territorio nazionale, per una superficie di circa 300000 km2 e un intervallo altitudinale compreso dal livello del mare fino alle vette più alte della catena alpina (M.te Bianco, 4810 metri circa). Anche la variabilità geomorfologica della penisola risulta molto varia con ambienti metamorfici, calcarei, vulcanici, alluvionali, ecc. e gran parte del territorio sviluppato lungo le coste dei mari tirreno, ionio ed adriatico.
Proprio questa complessità locale sembra influenzare il modello climatico generale tipico del mediterraneo, il quale presenta estati calde ed aride specialmente lungo le coste e periodi di freddo invernale prolungato ed intenso con precipitazioni abbondanti nelle zone più interne delle catene montuose.
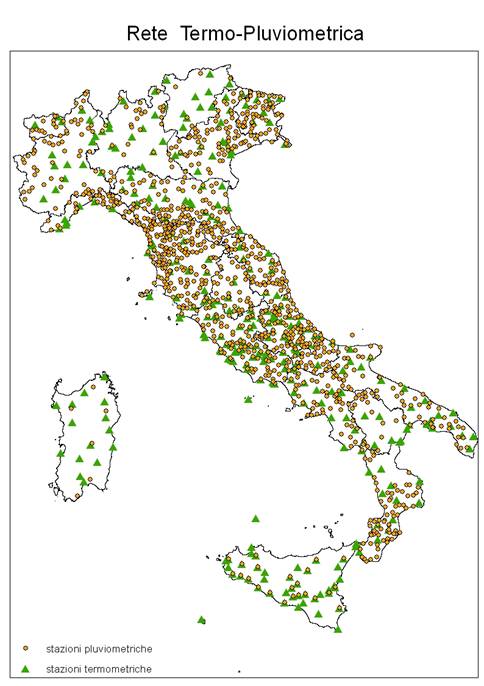
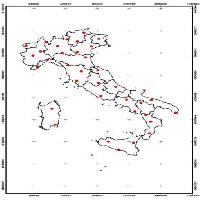
I dati climatici, rappresentati da medie mensili relative al trentennio 1961-1990, sono stati ottenuti dall’elaborazione statistica di dati meteorologici provenienti da una rete di rilevamento su scala nazionale composta da 1102 stazioni pluviometriche e 321 stazioni termometriche (Fig. 1).
Sono stati inoltre elaborati diversi indici bioclimatici.
Quoziente pluviometrico di Emberger
Emberger ([15]), classifica il clima Mediterraneo sulla base di un quoziente pluviometrico (Q) attraverso la seguente formula (eqn. 1):
dove P = precipitazione annua; Tmax = media delle temperature massime dei mesi più caldi; Tmin = media delle temperature minime dei mesi più freddi.
Indici di stress da freddo e da caldo di Mitrakos
Mitrakos ([31]), ha elaborato due indici di stress per le piante. Il primo, summer drought stress index (SDS), definisce l’intensità e la durata dell’aridità estiva sulla base dei valori di precipitazione dei mesi di Giugno, Luglio e Agosto, il secondo, winter cold stress (WCS), quantifica lo stress da freddo sulla base dei valori di temperatura minima dei mesi di Dicembre, Gennaio e Febbraio (eqn. 2).
dove Ps = media delle precipitazioni medie di Giugno, Luglio e Agosto (eqn. 3);
dove Tminw = media delle temperature minime di Dicembre, Gennaio e Febbraio
Indici bioclimatici di Rivas-Martinez
Rivas-Martinez ([37], [38]), individua sulla base delle combinazioni di indici climatici la regione climatica di appartenenza.
Indice ombrotermico estivo compensato (COSi)
Indice di continentalità (Ci)
dove Tmax e Tmin rappresentano le temperature medie del mese più caldo (Luglio) e del mese più freddo (Gennaio).
Indice di termicità (Ti)
dove T = temperatura media annua; m = media delle temperature minime del mese più freddo; M = media delle temperature massime del mese più freddo.
Indice di aridità estiva di De Martonne
De Martonne ([13]), elabora un indice di aridità estiva (Ai) basato sulla lunghezza del periodo arido estivo definito dalla seguente formula (eqn. 7):
dove P = precipitazione media annua; T = temperatura media annua.
Le variabili climatiche e bioclimatiche considerate per le analisi sono elencate nella Tab. 1. Come variabili indipendenti sono state utilizzate: altitudine (ALT), esposizione (ASP), pendenza (SLO), latitudine (LAT), longitudine (LON), continentalità (CON) e un indice mensile e annuale di radiazione solare stimata (ESR) ottenuto mediante l’applicazione di un modulo del software GIS GRASS. La procedura di interpolazione mediante kriging è stata ricavata da librerie del software statistico R (Maptools, Gstat, GeoR, Sgeostat, Randomfields ed altre). La restituzione cartografica in formato GRID con una risoluzione di 500 m è stata prodotta utilizzando il modulo Spatial Analiyst di ArcGIS 9.1 della ESRI.
Tab. 1 - Variabili analizzate: legenda e statistiche descrittive.
| Variabili | Descrizione | Min | I Qu | Mediana | Media | III Qu | Max |
|---|---|---|---|---|---|---|---|
| P5 | Precipitazioni di Maggio | 12 | 53 | 70 | 81 | 96 | 326 |
| P6 | Precipitazioni di Giugno | 0 | 43 | 57 | 69 | 82 | 287 |
| P7 | Precipitazioni di Luglio | 1 | 28 | 41 | 49 | 58 | 210 |
| P8 | Precipitazioni di Agosto | 6 | 42 | 60 | 69 | 86 | 248 |
| Ptot | Precipitazioni annuali | 394 | 790 | 962 | 1064 | 1256 | 3092 |
| Tm5 | Temperatura media di Maggio | -4.9 | 15.1 | 16.8 | 15.9 | 17.7 | 19.9 |
| Tm6 | Temperatura media di Giugno | -1.6 | 19.0 | 20.6 | 19.8 | 21.6 | 24.3 |
| Tm7 | Temperatura media di Luglio | 0.8 | 21.9 | 23.3 | 22.6 | 24.5 | 27.2 |
| Tm8 | Temperatura media di Agosto | 0.6 | 21.6 | 23.2 | 22.5 | 24.5 | 27.6 |
| Tm | Temperatura media annuale | -6.2 | 12.4 | 14.2 | 13.7 | 16.0 | 19.0 |
| Tmax 7 | Temp. media max. del mese più caldo | 3.4 | 27.3 | 28.9 | 28.2 | 30.0 | 34.2 |
| Tmin 1 | Temp. media min. del mese più freddo | -14.4 | -0.4 | 2.5 | 2.1 | 4.9 | 10.2 |
| Q | Quoziente pluviometrico | 43.8 | 83.0 | 98.6 | 117.6 | 137.6 | 554.5 |
| SDS | Indice di stress da aridità estiva | -396 | -48 | -6 | -24 | 24 | 92 |
| WCS | Indice di stress da freddo invernale | -4.8 | 36.8 | 56.0 | 58.3 | 76.0 | 192.8 |
| COSi | Indice ombrotermico estivo compensato | 0.3 | 1.2 | 2.1 | 2.3 | 2.9 | 9.8 |
| Ci | Indice di continentalità | 11.6 | 15.5 | 16.9 | 17.0 | 18.3 | 23.0 |
| Ti | Indice di termicità | -301 | 183 | 259 | 249 | 330 | 438 |
| Ai | Indice di aridità | 14.1 | 28.5 | 34.4 | 38.9 | 45.9 | 104.1 |
Metodo di interpolazione
I metodi di interpolazione che possono essere utilizzati per la spazializzazione di dati climatici si dividono in due principali tipologie: tecniche deterministiche e tecniche stocastiche, le prime operano sulla base di formule matematiche che calcolano medie pesate dei valori vicini conosciuti (per esempio la distanza inversa pesata e le regressioni polinomiali globali e locali), le seconde effettuano predizioni attraverso medie pesate e con l’ausilio di modelli probabilistici (per esempio il kriging).
La scelta di quale tecnica usare è spesso un compromesso tra le prestazioni del modello valutate in base alla sua capacità di adattarsi ad un set di validazione e la complessità del modello stesso in termini di capacità di interpretazione e facilità di ottenere stime. Il kriging in linea generale rappresenta un metodo di regressione che permette di interpolare e quindi di predire un valore nello spazio riducendo al minimo l’errore quadratico medio. Partendo dal valore conosciuto per alcuni punti nello spazio è possibile determinare il valore per tutti gli altri punti non noti mediante l’assunto che la grandezza in oggetto possa variare con continuità secondo la prima legge della geografia di Tobler.
La base del kriging è data dal semivariogramma che esprime le differenze spaziali e quantitative di tutte le possibili coppie di punti misurati come una funzione della distanza fra i punti stessi (eqn. 8):
dove γ(h) è la semivarianza della variabile Z alla distanza h mentre N(h) rappresenta il numero di coppie di punti nell’intervallo considerato.
I valori del semivariogramma vengono calcolati per ogni coppia di punti e successivamente un semivariogramma medio viene espresso graficamente rispetto alla distanza h producendo così un variogramma empirico. Quest’ultimo viene adattato utilizzando un modello parametrico che include stazionarità e isotropia (quest’ultima se necessaria), e il miglior modello parametrico viene usato per la costruzione della matrice di auto-covarianza dei residui della regressione.
In questo modo i modelli di kriging ordinario e semplice possono essere così definiti (eqn. 9):
dove z(si) è un processo stazionario intrinseco, mentre m è una tendenza costante non conosciuta (localmente) del kriging ordinario.
Una più ampia tipologia di modelli viene ottenuta quando l’osservazione z(si) risulta stimata dalla somma della tendenza m(si), spazialmente non costante, con un errore e (si) intrinsecamente stazionario.
In particolare nell’UK ([42]) questo tipo di tendenza può essere calcolato come una funzione lineare di p variabili predittive (covariate climatiche, geografiche e topografiche) e p costanti sconosciute βj che determinano per l’osservazione a si (eqn. 10):
dove Xj (si) , j=1, …, p rappresenta i valori delle covariate misurate all’i-esimo punto nella griglia.
Questo modello è simile ad un modello di regressione lineare standard con l’aggiunta di un termine di errore, e (si) , che non si suppone più essere indipendente da e (si), con i diverso da j = 1, …, n. Con i dati spaziali, i residui sono sicuramente correlati spazialmente, e data la matrice di (auto-) covarianza V di e (s) , la migliore predizione BLUP (best linear unbiased predictor) di Z (s0) ad un punto non misurato s0 sarà data da (eqn. 11, eqn. 12):
dove xj (s0) è il valore j-esimo della covariata in s0, βj è la stima generalizzata dei minimi quadrati del coefficiente di tendenza, e v è uguale a (Cov (Z (s0),Z (s1)),..., Cov (Z (s0), Z (sn)))’.
Qui, Cov (·, ·) denota covarianza e v’ è la trasposizione di v. A differenza delle procedure deterministiche, quelle basate sul kriging forniscono sia le deviazioni standard che i relativi intervalli di confidenza per le stime dei punti non misurati. Mentre il kriging è conosciuto come best linear unbiased predictor (BLUP), si riscontrano a volte problemi di non stazionarietà dei dati misurati che potrebbero limitarne la sua applicabilità.
Piuttosto che utilizzare UK con una tendenza definita attraverso un set di covariate, alcuni Autori ([1], [33], [2]) hanno proposto un approccio semplificato basato su Regression Kriging (RK), cioè un kriging after de-trending, dove la funzione di tendenza e i residui stimati vengono modellati separatamente.
Questo metodo è basato su una regressione lineare governata dall’ipotesi che i residui siano campioni indipendenti dallo stesso errore di distribuzione, con 0 di media e varianza costante. Tuttavia i residui della regressione risultano di fatto correlati, e questa è la ragione per utilizzare RK anziché della semplice regressione.
In questo contesto i coefficienti di stima potrebbero essere influenzati non correttamente, il variogramma dei residui potrebbe essere modellato insufficientemente e, infine, la predizione potrebbe risultare sbagliata.
Se i punti campione sono raggruppati in alcune parti della mappa (cosa frequente nelle analisi geografiche), potremmo stimare non correttamente i coefficienti di regressione a causa del fatto che i punti campione non sono stati pesati. Ovviamente tale problema potrebbe non essere osservato nelle applicazioni empiriche, a meno che non venga utilizzato un test set, così da applicare una effettiva comparazione delle caratteristiche di predizione dei vari metodi ([12]).
Risultati e discussione
L’insieme dei dati climatici è stato diviso in maniera del tutto casuale in due gruppi: il primo, composto dal 70% delle stazioni, è stato utilizzato come test set, il secondo, composto dal rimanente 30%, è stato utilizzato come set di validazione. Come raggi di calcolo sono stati scelti 15 e 30 km che già in un precedente lavoro ([3]) si erano dimostrati essere i migliori per questo tipo di analisi.
Per la stima delle variabili climatiche e bioclimatiche sono state effettuate venti elaborazioni basate su altrettanti gruppi differenti. In Tab. 2 è riportato, per ogni variabile il valore medio dalla Radice dell’Errore Quadratico Medio (RMSE, Root Mean Square Error) e la relativa deviazione standard.
Tab. 2 - Media delle 20 elaborazioni dell’RMSE assoluto e relativo (%) per ciascuna variabile.
| Variabile | Range 15 km | Range 30 km | ||
|---|---|---|---|---|
| Assoluto | Relativo | Assoluto | Relativo | |
| P5 | 13.34 | 3.6 | 14.04 | 4.1 |
| P6 | 6.42 | 2.4 | 9.99 | 3.5 |
| P7 | 8.08 | 3.5 | 8.94 | 4.6 |
| P8 | 11.41 | 9.18 | 9.18 | 8.2 |
| PTOT | 119.24 | 6.3 | 120.14 | 7.7 |
| TM5 | 0.74 | 2.8 | 0.72 | 2.1 |
| TM6 | 0.80 | 1.7 | 0.68 | 1.5 |
| TM7 | 0.79 | 1.1 | 0.80 | 2.3 |
| TM8 | 0.85 | 2.9 | 0.81 | 2.3 |
| TM | 0.74 | 2.4 | 0.73 | 2.3 |
| TMAX7 | 1.38 | 1.5 | 1.31 | 1.2 |
| TMIN1 | 0.75 | 9.7 | 0.71 | 8.8 |
| Q | 55.10 | 10 | 58.89 | 11.4 |
| SDS | 11.66 | 5.5 | 18.77 | 8.3 |
| WCS | 5.85 | 5.9 | 5.16 | 4.8 |
| COSi | 0.46 | 3.8 | 0.44 | 2.9 |
| Ci | 0.63 | 0.8 | 0.61 | 0.5 |
| Ti | 14.92 | 3.4 | 14.87 | 2.8 |
| Ai | 28.22 | 9 | 33.07 | 10.3 |
Dai valori di RMSE presenti in Tab. 2 è possibile evincere che le variabili delle precipitazioni (Maggio, Giugno e Luglio, e le precipitazioni annuali) così come gli indici, nel cui calcolo sono utilizzate le precipitazioni (Q, SDS), sono stimate in maniera migliore utilizzando un raggio di calcolo di 15 km. Al contrario per le variabili di temperatura e gli indici bioclimatici basati solo su di esse (WCS, Ci, Ti) il raggio a 30 km risulta il più idoneo. Solo per il valore delle temperature del mese di Agosto, il risultato migliore è relativo al raggio di 15 km. Tale risultato può essere spiegato tenendo in considerazione che le precipitazioni sono influenzate anche da fattori locali legati alla geomorfologia del territorio mostrando così una maggiore variabilità spaziale che può essere spiegata meglio da un raggio ridotto (15 km). Al contrario le temperature presentano un andamento legato principalmente alle variazioni altitudinali e latitudinali e quindi possono essere stimate in maniera efficace da un intervallo spaziale maggiore.
Conclusioni
Il kriging universale con deriva esterna e uso di covariate (longitudine, latitudine, altitudine, pendenza, esposizione, continentalità e radiazione solare stimata) si è dimostrato un interpolatore di dati climatici e bioclimatici efficiente e computazionalmente veloce dell’ordine di alcuni minuti per elaborare le stime e le predizioni relative alle 20 ripetizioni utilizzate. Applicando l’UK all’intero set di dati sono state prodotte 52 carte climatiche relative alle medie mensili e annuali delle precipitazioni e delle temperature minime, massime e medie, e 7 carte bioclimatiche. In particolare il raggio di 15 km è stato utilizzato per la produzione cartografica relativa alle 13 variabili legate alle precipitazioni e ai 4 indici bioclimatici contenenti variabili di precipitazione, e quello di 30 Km per l’elaborazione delle 39 carte relative alle temperature e dei relativi indici bioclimatici.
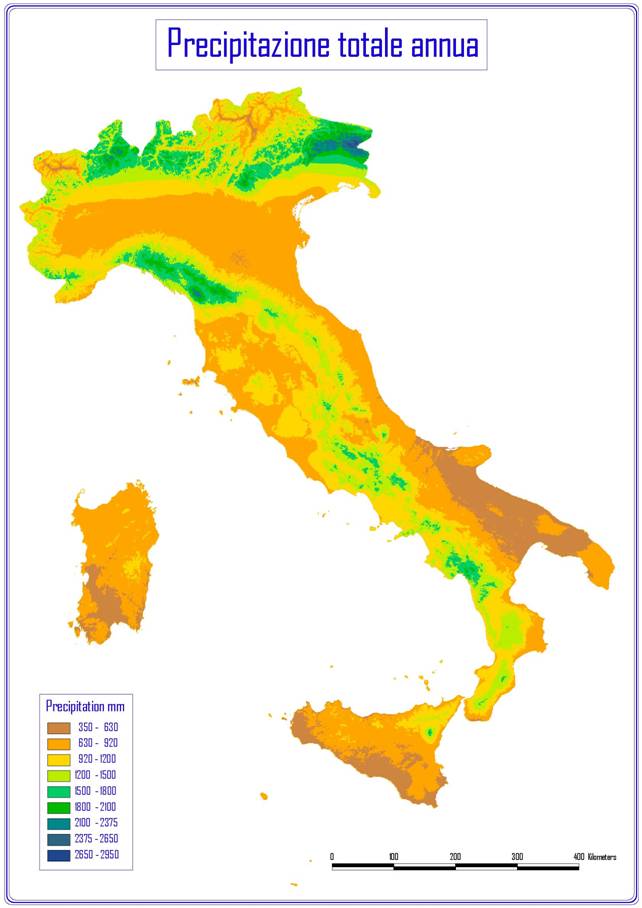
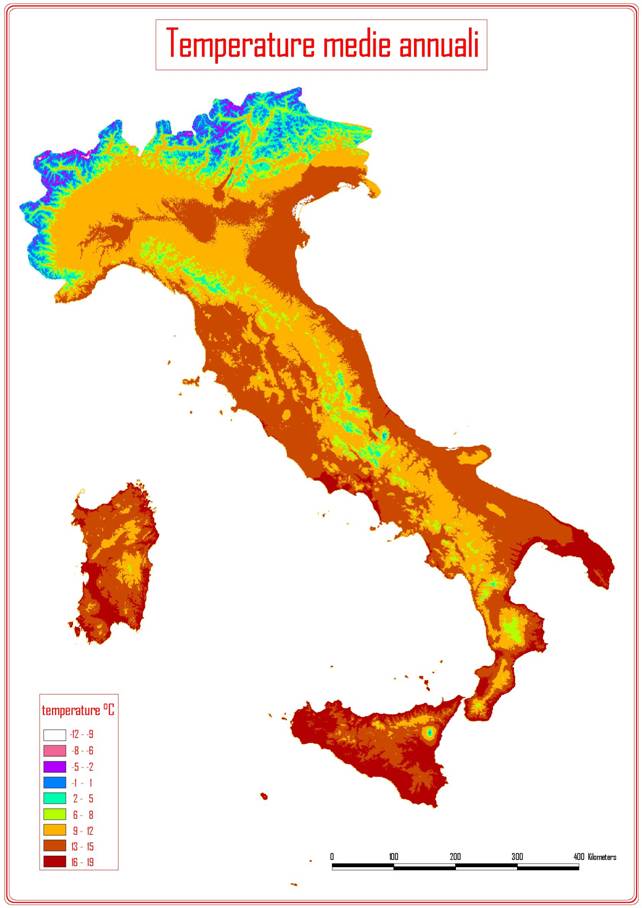
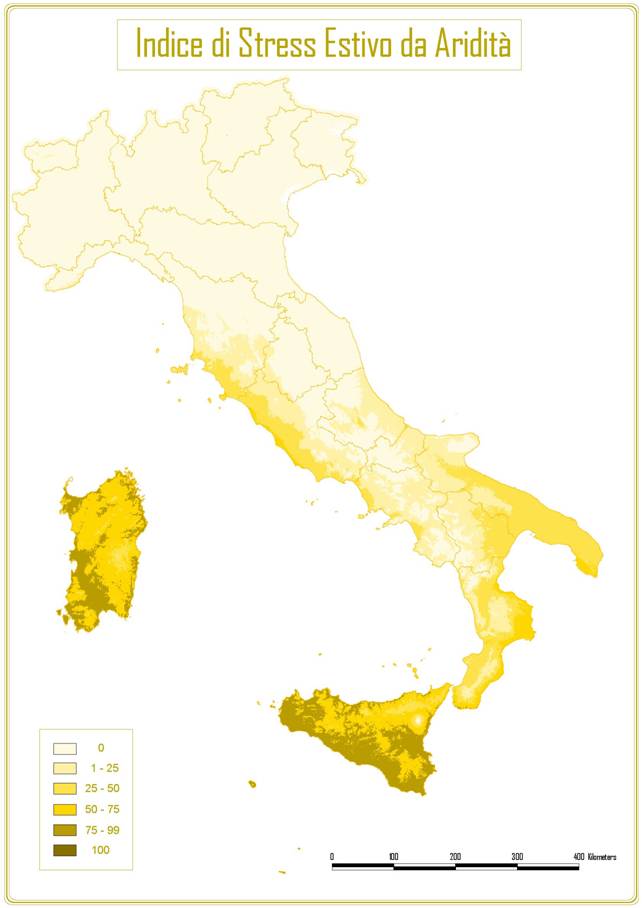
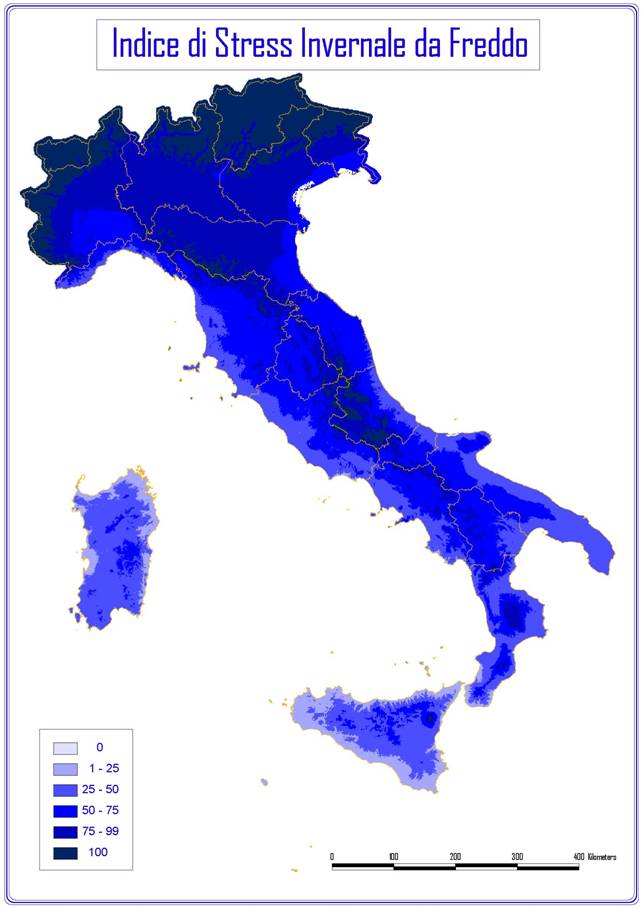
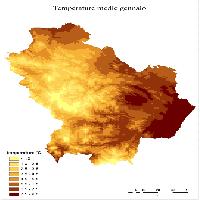
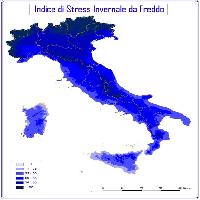
A titolo di esempio sono riportate in Fig. 2, Fig. 3, Fig. 4 e Fig. 5 rispettivamente la carta delle precipitazioni annue, della temperatura media annua, dell’indice di stress da aridità estiva (SDS) e dell’indice da stress invernale da freddo (WCS) di Mitrakos. Le mappe in formato GRID con una risoluzione di 500 m sono utilizzabili in molteplici settori applicativi dalla pianificazione ambientale alla valutazione dei potenziali effetti dei cambiamenti climatici su specie ed ecosistemi.
Ringraziamenti
Il lavoro è stato portato avanti nell’ambito del progetto CONECO-FOR (CONtrollo ECOsistemi FORestali), il programma di monitoraggio intensivo degli ecosistemi forestali in Italia. Tale programma è inserito all’interno del Pan-European Level II Monitoring of Forest Ecosistems, sponsorizzato dall’Unione Europea dal Regolamento n. 2152/2003 “Forest Focus” e coopera con il UN/ECE ICP-Forest e il UN/ECE ICP-Integrated Monitoring of Ecosystems. CONECOFOR è diretto dal Corpo Forestale dello Stato, Divisione 6a, CONECOFOR Board, fungendo anche da National Focal Centre (NFC) insieme alla Comunità Europea e alle Nazioni Unite nell’ambito del programma UN/ECE.
References
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Online | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Online | Google Scholar