Spatial interpolation methods for monthly rainfalls and temperatures in Basilicata
Forest@ - Journal of Silviculture and Forest Ecology, Volume 5, Pages 337-350 (2008)
doi: https://doi.org/10.3832/efor0550-0050337
Published: Dec 12, 2008 - Copyright © 2008 SISEF
Research Articles
Abstract
Spatial interpolated climatic data on grids are important as input in forest modeling because climate spatial variability has a direct effect on productivity and forest growth. Maps of climatic variables can be obtained by different interpolation methods depending on data quality (number of station, spatial distribution, missed data etc.) and topographic and climatic features of study area. In this paper four methods are compared to interpolate monthly rainfall at regional scale: 1) inverse distance weighting (IDW); 2) regularized spline with tension (RST); 3) ordinary kriging (OK); 4) universal kriging (UK). Besides, an approach to generate monthly surfaces of temperatures over regions of complex terrain and with limited number of stations is presented. Daily data were gathered from 1976 to 2006 period and then gaps in the time series were filled in order to obtain monthly mean temperatures and cumulative precipitation. Basic statistics of monthly dataset and analysis of relationship of temperature and precipitation to elevation were performed. A linear relationship was found between temperature and altitude, while no relationship was found between rainfall and elevation. Precipitations were then interpolated without taking into account elevation. Based on root mean squared error for each month the best method was ranked. Results showed that universal kriging (UK) is the best method in spatial interpolation of rainfall in study area. Then cross validation was used to compare prediction performance of tree different variogram model (circular, spherical, exponential) using UK algorithm in order to produce final maps of monthly precipitations. Before interpolating temperatures were referred to see level using the calculated lapse rate and a digital elevation model (DEM). The result of interpolation with RST was then set to originally elevation with an inverse procedure. To evaluate the quality of interpolated surfaces a comparison between interpolated and measured temperatures at eight sites from an independent dataset was done. There was a good agreement with mean R2=0.99 (mean RMSE=0.6°C). Based on this results universal kriging estimates and RST were used to produce monthly rainfall and temperature maps for Basilicata region aimed at using as quality input in forest modeling.
Keywords
Climate, Spatial interpolation, Kriging, Rainfall, Temperature, Geostatistics, Lapse-rate
Introduzione
La modellistica ambientale in generale e forestale in particolare, ha sviluppato, negli ultimi anni, numerosi e differenziati modelli di stima e di analisi spaziale che necessitano di dati georiferiti ([37], [10], [11], [33], [25]); tra questi, quelli climatici ricoprono un ruolo fondamentale in quanto il clima ha effetti diretti sia sulla produttività che sulla diffusione dei diversi biomi terrestri ([34]).
Tra i diversi metodi riconosciuti come efficienti predittori nella stima degli andamenti delle temperature e delle precipitazioni vanno menzionati l’inverso della distanza pestata, lo spline, il kriging e le sue possibili modulazioni, il co-kriging, le reti neurali e i più recenti modelli regressivi localizzati ([3]).
L’ottenimento di superfici climatiche richiede l’applicazione di tecniche d’interpolazione differenziate in funzione della variabile considerata, della qualità dei dati in ingresso, della numerosità delle stazioni di registrazione, della loro posizione geografica e della complessità orografica del territorio di indagine ([20]). In linea generale, quando i dati di base sono numerosi e ben distribuiti, tutti i metodi restituiscono risultati statisticamente accettabili ([4], [17]). Più frequente è però il caso di territori con caratteristiche morfo-topografiche complesse e con un’esigua numerosità delle stazioni di rilevazione. In questo caso l’interpolazione deve essere preceduta da un’attenta analisi delle variabili climatiche e delle caratteristiche topografiche per individuare preliminarmente le modalità più efficienti per affrontare le successive fasi di elaborazione.
Non esistono metodi in genere migliori di altri ma, per ciascun singolo caso di studio, deve essere fatta un’attenta valutazione per individuare quelli in grado di minimizzare l’errore di stima. Collins & Bolstad ([9]), per esempio, hanno confrontato otto metodi d’interpolazione delle temperature a tre differenti scale temporali, concludendo che diverse caratteristiche delle variabili in ingresso, come l’intervallo di acquisizione, la varianza e la correlazione con altre variabili ambientali, possono influire sulla scelta delle tecniche di interpolazione.
Per l’interpolazione dei dati climatici esistono diversi metodi tra quelli di tipo deterministico (ad es., IDW, spline) e quelli di tipo stocastico (ad es., kriging e co-kriging - [22], [23]). Tra i secondi il kriging sembra presentare le migliori possibilità applicative in climatologia ([2]), anche se ha lo svantaggio di richiedere una certa esperienza da parte dell’operatore: la costruzione del semivariogramma sperimentale, la scelta del variogramma teorico e del numero dei neighborhoods ([4]) sono tutte operazioni che influiscono sul risultato finale. Tra i vantaggi ha quello di basarsi su concetti statistici per modellare la natura spaziale della variazione fornendo anche una stima degli errori commessi nel processo di interpolazione.
Gli interpolatori di tipo deterministico usano funzioni matematiche per modellare la natura spaziale dei fenomeni. L’inverso della distanza pesata attribuisce i pesi ai punti non campionati soltanto in funzione della distanza rispetto ai punti noti ([32]). Le funzioni spline sono, tra gli interpolatori di tipo deterministico, quelli più complessi e hanno, come tutti gli interpolatori di questa categoria, il limite di non fornire una stima degli errori ([21]). Tuttavia sono metodi relativamente semplici e veloci, richiedono il settaggio di pochi parametri e non necessitano che i dati siano correlati nello spazio. Quando i punti campionati sono numerosi e distribuiti in modo uniforme sul territorio possono fornire risultati soddisfacenti, comparabili a quelli ottenuti con tecniche di tipo stocastico ([20]).
Il presente lavoro è finalizzato all’individuazione delle metodologie più idonee all’interpolazione di alcune variabili climatiche (precipitazioni e temperature medie mensili) della Basilicata e all’ottenimento di strati informativi di qualità funzionali allo sviluppo di una modellistica forestale efficiente.
Metodi d’interpolazione considerati
I metodi utilizzati sono brevemente descritti in questa sezione. Per un approfondimento degli argomenti trattati ci si può riferire a una ormai vasta letteratura ([26], [18], [35]).
Inverse distance weighting (IDW)
L’IDW è una stima pesata dei dati disponibili in uno specifico intorno. Può essere espresso con la seguente formula (eqn. 1):
dove la stima nel punto non noto u o è funzione dei punti dove la variabile è nota z(u α ), d è la distanza alla quale il punto u o è separato da ogni altra osservazione e r è un esponente. Come r aumenta il peso assegnato alle osservazioni a maggiore distanza diminuisce nella stima del valore finale di u o, in altre parole u o dipende in misura maggiore dai punti più vicini.
Regularized spline with tension (RST)
L’RST è un metodo di interpolazione di tipo deterministico basato su funzioni matematiche complesse di tipo spline ([28], [27]).
È un metodo estremamente flessibile attraverso la scelta di alcuni parametri come la tension e lo smoothing ([21]). La tension è forse il parametro più importante in relazione al risultato finale: controlla la dimensione delle interazioni tra regioni interpolate individualmente. Un alto valore di tension impone alla superficie la permanenza di un trend, per bassi valori avviene invece il contrario. Pensando la superficie interpolata come un foglio di gomma, il valore di tension permette di variare la flessibilità della membrana passando da una superficie sottile ed elastica ad una spessa e rigida. Lo smoothing è il parametro che consente l’eliminazione di eventuali “rumori”; definisce quanto la superficie interpolata debba passare vicino ai punti noti; un valore di smoothing pari a zero impone il passaggio della superficie per il punto osservato, portando a volte a superfici innaturali. Questo parametro può essere configurato anche in funzione dell’affidabilità dei dati misurati. Mentre l’IDW utilizza una funzione lineare per ciascuno degli intervalli compresi tra i valori di due punti noti, l’interpolatore spline si serve, nei suddetti intervalli, di polinomi di piccolo grado raccordati tra di loro.
Il kriging
Il cuore dell’analisi geostatistica è rappresentato dal variogramma, che descrive la dipendenza spaziale nei dati studiati. Il variogramma è pari alla semi-differenza quadrata tra coppie di valori che si trovano ad una certa distanza. In pratica si calcola la media della differenza quadrata di tutte le coppie di valori che si trovano ad una data distanza (per esempio 10-20 km) e queste differenze medie quadrate vengono poi riportate su un piano in funzione della distanza. Il semivariogramma sperimentale può essere stimato per ciascuna coppia di valori p(h) (eqn. 2):
dove z(u o ) è il valore della variabile oggetto di studio nei due punti separati da una distanza h, definita anche come lag.
Un modello matematico può essere dopo adattato al variogramma sperimentale e i coefficienti di questo modello usati per il kriging. Nei modelli di variogramma quando la semi-varianza raggiunge ad una distanza finita il valore massimo viene definito il sill (c 1) che è una proprietà dei modelli di tipo sferico ed esponenziale. Il lag al quale viene raggiunto il sill, che è il limite della dipendenza spaziale del variogramma, è chiamato range. In alcuni modelli il sill non viene mai raggiunto, ne è un esempio il modello di tipo esponenziale. Questi modelli indicano la presenza di una tendenza presente a grande scala nei valori studiati. In teoria, la semivarianza per un lag pari a zero dovrebbe essere zero. In pratica, succede che questo valore è positivo e pari ad una certa quantità definita nugget. Il nugget può essere ascrivibile ad errori di misurazione oppure alla scala di campionamento che magari non è tanto piccola da riuscire ad individuare le differenze tra i diversi valori a breve distanza.
Le stime fatte dal kriging, a parità dell’IDW, sono medie pesate dei dati disponibili, la differenza è che i dati sono usati per descrivere il grado e la forma della dipendenza spaziale che viene modellata e usata per poi assegnare il peso alle diverse osservazioni mentre per l’IDW il peso viene assegnato in modo arbitrario, solo in relazione alla distanza. I pesi assegnati con il kriging sono definiti come best linear unbiased estimator (BLUE).
La stima ottenuta con il kriging - z(u o ) -, è una media lineare pesata mobile delle osservazioni n disponibili ed è definita come (eqn. 3):
L’obiettivo è quindi quello di cercare il peso λ α per il quale le osservazioni sono moltiplicate per una costante e la somma dei pesi sia pari a uno.
La differenza principale tra i due tipi di kriging utilizzati in questa tesi, ordinary kriging (OK) e universal kriging (UK) è nel modo di calcolare la media mobile pesata dei punti campionati: nell’OK la media è sconosciuta e costante, nell’UK la media è sostituita da una funzione di tipo deterministico.
Base di dati
L’area di studio è la Basilicata compresa tra i 15°20’ e i 16°53’ di latitudine e i 39°54’ e i 41°8’ di longitudine est. La superficie di 10000 km2 è composta per il 70% dall’Appennino. La quota varia da 0 a 2400 m s.l.m. ([14]). Il clima è di tipo mediterraneo, con precipitazioni distribuite irregolarmente durante l’anno e con un’elevata variabilità interannuale. Nella zona sud-ovest, quella che si affaccia sul tirreno, il clima è più continentale con precipitazioni che superano abbondantemente i 2000 mm anno-1, mentre lungo la fascia jonica è possibile rinvenire aree con precipitazioni inferiori ai 500 mm anno-1. Il sistema appenninico attribuisce diverse influenze climatiche in quanto costituisce una barriera alla traiettoria delle perturbazioni atlantiche nel Mediterraneo facendo da spartiacque tra i bacini del mar Tirreno e quello del mar Jonio e determinando una differenza evidente tra le due provincie. Le particolari condizioni altimetriche della provincia di Potenza unite a questo effetto producono, anche nell’ambito della stessa regione, una cospicua varietà di climi ([13]). Nell’ambito della penisola italiana la Basilicata si inserisce tra le isoterme annuali 5°-16°. Le varie località pur a latitudini abbastanza meridionali registrano temperature medie annue piuttosto basse e minime al di sotto dello zero nelle zone a maggior quota; gli inverni sono rigidi e le estati relativamente calde e con escursioni notevoli.
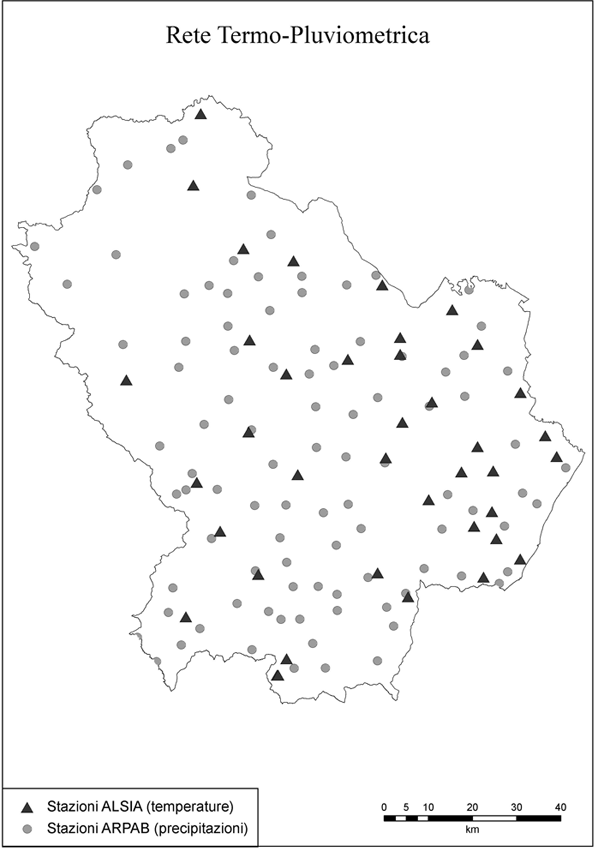
I dati meteorologici giornalieri sono costituiti da misurazioni acquisite da stazioni afferenti alle reti dell’ARPAB e all’ALSIA della Basilicata (Fig. 1). I dati grezzi sono stati elaborati e le misurazioni mancanti colmate con una procedura di gap-filling basata sulla correlazione locale tra stazioni vicine ([16]). Per ogni stazione sono stati calcolati i valori climatici medi mensili riferiti alle precipitazioni e alle temperature. Le 97 stazioni ARPAB con un periodo di acquisizione riferito al trentennio 1976-2006 sono state usate per l’interpolazione delle precipitazioni. Per quanto riguarda le temperature si è invece optato per l’uso del dataset ALSIA composto da 39 stazioni termometriche con acquisizioni riferite al decennio 1996-2006. Le stazioni termometriche ARPAB con acquisizioni continue negli ultimi 30 anni sono infatti soltanto 20, un numero troppo basso per una efficiente interpolazione spaziale dei dati, considerata anche l’orografia del territorio in esame. L’uso di dati basati su 10 anni contrasta con le indicazioni della WMO che consiglia di interpolare dati su una media di almeno 30 anni; l’interpolazione delle temperature è dunque solo indicativa della tecnica applicata.
Analisi dei dati
I dati mensili sono stati elaborati con il software Statistica 6.0 ([5]).
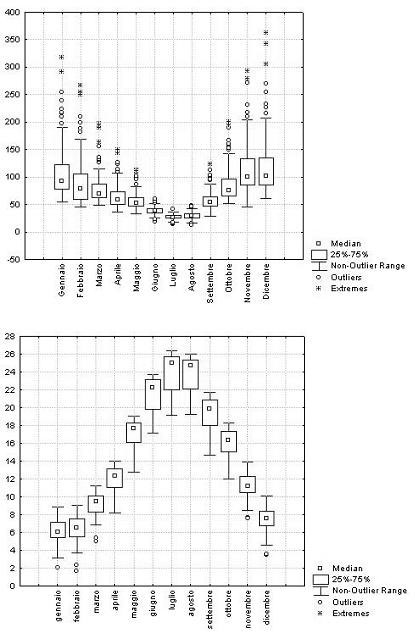
La Tab. 1 e la Tab. 2 riportano le analisi statistiche descrittive delle precipitazioni e delle temperature eseguite sui dati mensili. In Fig. 2 sono rappresentati i grafici box-plot dai quali si evince che dicembre è il mese più piovoso mentre luglio il più secco. Luglio è anche il mese più caldo, gennaio il più freddo. Ad eccezione dei mesi estivi è evidente una certa asimmetria nelle precipitazioni, mentre avviene il contrario per le temperature. Altre indicazioni sull’andamento dei dati sono fornite dalla curtosi e dal grado di skewness. Se per le temperature le differenze tra valori massimi e valori minimi sono contenute tra i 3 e i 5 °C per le precipitazioni l’intervallo può essere superiore ai 300 mm mese-1. Questo conferma che nella regione esistono diversi regimi pluviometrici. Nei grafici box-plot sono presenti outliers, punti con valori anomali rispetto alla distribuzione. Per quanto riguarda le precipitazioni gli outliers sono tutti individuabili in stazioni presenti nell’area sud-ovest. L’anomalia è quindi dovuta ad una situazione reale e non ad errori di misurazione o di calcolo dei dati mensili.
Tab. 1 - Analisi statistiche descrittive delle precipitazioni mensili (SE=Standard Error; Std. Dev=Deviazione Standard: SV=varianza campionaria).
| Parametri | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | P12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Media | 109.9 | 91.9 | 80.4 | 64.9 | 57.9 | 38.9 | 27.0 | 29.5 | 59.2 | 88.0 | 115.6 | 122.0 |
| SE | 5.4 | 4.8 | 3.1 | 2.5 | 1.7 | 0.7 | 0.5 | 0.7 | 1.9 | 3.3 | 4.8 | 5.9 |
| Mediana | 91.0 | 78.0 | 70.0 | 58.0 | 53.0 | 38.0 | 27.0 | 29.0 | 54.0 | 75.0 | 100.0 | 102.0 |
| Moda | 84.0 | 50.0 | 59.0 | 47.0 | 60.0 | 37.0 | 25.0 | 28.0 | 50.0 | 64.0 | 79.0 | 94.0 |
| Std.Dev | 53.2 | 47.6 | 30.7 | 24.5 | 17.2 | 7.1 | 4.9 | 6.5 | 18.8 | 32.3 | 47.2 | 58.4 |
| SV | 2826.4 | 2265.0 | 944.7 | 602.2 | 294.6 | 51.1 | 23.7 | 42.6 | 352.8 | 1040.5 | 2227.7 | 3413.5 |
| Curtosi | 3.3 | 3.2 | 4.8 | 2.9 | 1.9 | 0.7 | 0.6 | 0.8 | 2.6 | 2.6 | 3.5 | 4.8 |
| Skewness | 1.8 | 1.8 | 2.1 | 1.7 | 1.4 | 0.1 | -0.1 | 0.3 | 1.6 | 1.7 | 1.8 | 2.1 |
| Range | 268.0 | 221.0 | 149.0 | 114.0 | 80.0 | 41.0 | 27.0 | 35.0 | 95.0 | 150.0 | 247.0 | 302.0 |
| Minimo | 50.0 | 45.0 | 49.0 | 36.0 | 33.0 | 19.0 | 14.0 | 13.0 | 29.0 | 51.0 | 46.0 | 61.0 |
| Massimo | 318.0 | 266.0 | 198.0 | 150.0 | 113.0 | 60.0 | 41.0 | 48.0 | 124.0 | 201.0 | 293.0 | 363.0 |
| Somma | 10663.0 | 8914.0 | 7796.0 | 6299.0 | 5616.0 | 3774.0 | 2617.0 | 2858.0 | 5739.0 | 8534.0 | 11209.0 | 11836.0 |
Tab. 2 - Analisi statistiche descrittive delle temperature mensili (SE=Standard Error; Std. Dev=Deviazione Standard: SV=varianza campionaria; n/a = non disponibile).
| Parametri | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | T10 | T11 | T12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Media | 7.6 | 8.1 | 10.6 | 13.4 | 19.0 | 23.9 | 26.4 | 26.2 | 21.6 | 17.9 | 13.1 | 9.2 |
| SE | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Mediana | 7.7 | 8.1 | 10.6 | 13.4 | 19.1 | 23.8 | 26.5 | 26.1 | 21.8 | 18.0 | 13.1 | 9.2 |
| Moda | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | 8.7 |
| Std.Dev | 0.9 | 0.8 | 0.9 | 0.8 | 0.7 | 0.8 | 0.9 | 0.9 | 0.8 | 0.8 | 0.8 | 0.9 |
| SV | 0.8 | 0.6 | 0.8 | 0.7 | 0.5 | 0.7 | 0.8 | 0.8 | 0.6 | 0.6 | 0.6 | 0.7 |
| Curtosi | -0.1 | 0.6 | 1.4 | 2.7 | -0.1 | 0.7 | 0.2 | 0.0 | 1.0 | 0.6 | 0.6 | 0.2 |
| Skewness | -0.3 | 0.1 | 0.5 | -0.1 | -0.1 | 0.2 | 0.0 | 0.0 | 0.1 | -0.2 | -0.5 | 0.0 |
| Range | 3.7 | 3.8 | 4.5 | 4.9 | 3.2 | 3.9 | 4.2 | 3.7 | 3.8 | 3.9 | 3.8 | 4.0 |
| Minimo | 5.7 | 6.1 | 8.8 | 11.0 | 17.4 | 22.0 | 24.3 | 24.4 | 19.8 | 16.0 | 10.9 | 7.0 |
| Massimo | 9.5 | 10.0 | 13.3 | 15.9 | 20.6 | 25.9 | 28.5 | 28.1 | 23.7 | 19.9 | 14.7 | 11.0 |
| Somma | 295.2 | 315.9 | 413.9 | 521.3 | 740.6 | 930.6 | 1028.9 | 1020.7 | 844.3 | 696.4 | 509.4 | 357.1 |
Analizzando l’altitudine delle stazioni termometriche si nota che quella a quota più bassa è Policoro (6 m s.l.m.) mentre Castelsaraceno è quella ad altitudine più elevata (1015 m). La media altimetrica delle stazioni termometriche è di 373 m. La regione Basilicata ha un’altitudine media di circa 560 m. Questo semplice confronto indica una carente distribuzione delle stazioni che non riescono a rappresentare tutta la variabilità altitudinale della regione. Le stazioni pluviometriche hanno invece una media altitudinale di 569 m per cui risultano essere distribuite in modo omogeneo lungo il profilo verticale.
Gli outliers nel grafico delle distribuzioni delle temperature corrispondono alle stazioni di Laurenzana (938 m s.l.m.) e Castelsaraceno che sono insieme a Brindisi di Montagna le sole al di sopra dei 700 m tra quelle fornite dall’ALSIA.
Le analisi preliminari comprendono lo studio della possibile correlazione tra le variabili climatiche e la quota (Tab. 3). A scala regionale le precipitazioni non mostrano una relazione accettabile con la quota, come peraltro già riscontrato da Cantore et al. ([6]); le temperature hanno invece mostrato indici di Pearson altamente significativi, con una relazione negativa rispetto all’altitudine. Tramite analisi di regressione lineare semplice è stato calcolato il lapse-rate (Tab. 4). I valori indicano abbassamenti di temperatura compresi tra -0.4 e -0.6 °C per ogni 100 metri. Questo risultato conferma quello di altri lavori ([29], [6], [7]).
Tab. 3 - Coefficiente di Pearson (r) tra altitudine delle stazioni e le precipitazioni e temperature medie mensili.
| Mesi | Precipitazioni | Temperature medie |
|---|---|---|
| Gennaio | 0.17 | -0.80 |
| Febbraio | 0.26 | -0.84 |
| Marzo | 0.22 | -0.79 |
| Aprile | 0.34 | -0.80 |
| Maggio | 0.37 | -0.86 |
| Giugno | 0.46 | -0.87 |
| Luglio | 0.55 | -0.86 |
| Agosto | 0.42 | -0.86 |
| Settembre | 0.25 | -0.86 |
| Ottobre | 0.20 | -0.83 |
| Novembre | 0.23 | -0.82 |
| Dicembre | 0.20 | -0.79 |
Tab. 4 - Relazione tra altitudine e temperatura espressa come lapse-rate.
| Mese | R2 | Lapse-rate 100 metri |
|---|---|---|
| Gennaio | 0.722 | -0.4 |
| Febbraio | 0.796 | -0.5 |
| Marzo | 0.690 | -0.4 |
| Aprile | 0.701 | -0.4 |
| Maggio | 0.786 | -0.5 |
| Giugno | 0.813 | -0.6 |
| Luglio | 0.788 | -0.6 |
| Agosto | 0.773 | -0.6 |
| Settembre | 0.821 | -0.6 |
| Ottobre | 0.757 | -0.5 |
| Novembre | 0.761 | -0.5 |
| Dicembre | 0.717 | -0.5 |
Risultati
I dati delle precipitazioni sono stati interpolati usando i quattro metodi. A caso è stato escluso il 20% delle stazioni (test set), mentre le restanti stazioni sono state utilizzate per interpolare i dati (training set). Per ciascuna variabile è stata calcolata la media dell’RMSE per ogni mese ottenuta ripetendo le operazioni di interpolazione e validazione per 20 volte per ciascuno degli interpolatori considerati ([2]).
La scelta dell’esponente nell’IDW e dei parametri di tension e smoothing può significantemente incidere sul risultato dell’interpolazione mediante i due metodi. Per questo il valore ottimale è stato determinato cercando il valore che minimizzava la radice quadrata dell’errore stimato (RMSPE). Per il kriging si è proceduto alla determinazione prima del semivariogramma sperimentale e poi alla scelta del modello di variogramma teorico che meglio si adattava ai dati sperimentali.
Nella Tab. 5, relativa alle precipitazioni, i quattro metodi sono messi a confronto. Tutti i dati sono stati elaborati usando Geostatistical Analyst Tool in ArcGIS 9.1 ([15]).
Tab. 5 - Confronto tra i 4 metodi testati per l’interpolazione delle precipitazioni mensili (IDW=Inverse Distance Weighting; RST=Regularized Spline with Tension; OK=Ordinary Kriging; UK=Universal Kriging). Vengono riportati i valori medi dell’RMSE e tra parentesi la deviazione standard per ciascun mese dell’anno.
| Metodo | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | P12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IDW | 20.69 | 22.91 | 14.59 | 11.24 | 9.14 | 5.49 | 4.15 | 4.33 | 8.00 | 12.99 | 22.27 | 26.75 |
| (7.31) | (6.65) | (4.92) | (4.63) | (1.95) | (0.96) | (0.66) | (0.57) | (1.49) | (3.19) | (4.16) | (8.29) | |
| RST | 20.77 | 23.34 | 14.91 | 11.25 | 9.03 | 5.36 | 4.14 | 4.25 | 7.84 | 12.75 | 21.74 | 26.23 |
| (7.52) | (7.10) | (5.26) | (3.89) | (1.85) | (0.92) | (0.67) | (0.54) | (1.49) | (3.15) | (3.60) | (8.13) | |
| OK | 19.38 | 22.07 | 14.53 | 10.80 | 8.95 | 5.38 | 4.05 | 4.27 | 7.81 | 12.46 | 21.33 | 25.10 |
| (7.36) | (7.52) | (5.04) | (4.16) | (1.78) | (0.91) | (0.69) | (0.50) | (1.42) | (2.99) | (4.40) | (8.03) | |
| UK | 19.21 | 21.80 | 14.57 | 10.98 | 8.81 | 5.29 | 4.05 | 4.27 | 7.54 | 12.32 | 21.02 | 25.16 |
| (7.35) | (7.63) | (4.91) | (4.61) | (1.78) | (0.87) | (0.68) | (0.50) | (1.32) | (3.10) | (4.79) | (8.31) |
È evidente che l’UK e l’OK restituiscono risultati migliori rispetto ai due metodi deterministici. La differenza è più evidente durante i mesi autunnali ed invernali quando le precipitazioni sono abbondanti e le differenze tra le diverse stazioni appartenenti ad aree climatiche differenti sono maggiori. Durante i mesi estivi invece l’RMSE è simile per i quattro metodi e, nel caso di agosto, è l’RST risulta più efficace. Nei mesi invernali le precipitazioni sono massime nell’area sud-ovest sottoposta alle correnti provenienti dal tirreno e bloccate dalle catene montuose che provocano quindi un raffreddamento e conseguenti precipitazioni proprio in quell’area. Spostandosi da ovest verso est e verso la costa jonica le precipitazioni mensili medie diminuiscono. Questo accade durante i mesi invernali e autunnali mentre nei mesi estivi sono soprattutto le influenze locali ad incidere di più sul clima e sulle precipitazioni. Dal punto di vista geostatistico quindi l’autocorrelazione spaziale degli eventi piovosi è meno evidente a scala regionale. I metodi deterministici non risentono di questa situazione.
L’UK è stato quindi scelto come miglior interpolatore delle precipitazioni medie mensili della Basilicata. Dal punto di vista operativo si è quindi proceduto all’interpolazione vera e propria delle precipitazioni con UK. I risultati sono sintetizzati nella Tab. 6 da cui è possibile trarre informazioni circa i modelli adottati, il range e la direzione dello stesso e soprattutto è possibile leggere una sintesi per ciascun modello dei risultati della cross-validation. La presenza di un range maggiore e uno minore è la causa di un’anisotropia spaziale dovuta alla distribuzione particolare delle piogge. La cross-validation, eseguita con una tecnica leave-one-out, indica che tutti i modelli forniscono buoni risultati con errori contenuti.
Tab. 6 - Modelli di interpolazione delle precipitazioni ottenuti con universal kriging. Le colonne indicano nell’ordine i mesi, il modello di variogramma matematico, il nugget, il range maggiore e quello minore, la direzione dell’anisotropia, il partial sill (differenza tra nugget e sill). Nella seconda sezione della tabella è riportata l’analisi di cross-validation (ME=errore medio; RMS=radice quadratica media dell’errore; MSE=media dell’errore standardizzato; MS=media standardizzata, RMSS=radice quadratica media standardizzata dell’errore).
| Mesi | Modello | Nugget | major range |
minor range |
Direzione (°) |
partial sill |
Cross validation | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (m) | (m) | (m) | ME | RMS | MSE | MS | RMSS | ||||
| P1 | sferico | 18.99 | 66986 | 52682 | 310 | 0.22 | -0.09 | 24.3 | 25.99 | 0 | 0.98 |
| P2 | sferico | 0 | 60401 | 52436 | 314 | 0.14 | -0.06 | 21.9 | 20.47 | 0.01 | 0.93 |
| P3 | sferico | 0 | 63650 | 52696 | 312 | 0 | 0 | 14.9 | 14.23 | 0.02 | 0.91 |
| P4 | sferico | 0 | 60533 | 54910 | 318 | 0.08 | 0.03 | 9.18 | 9.07 | 0 | 0.98 |
| P5 | sferico | 0 | 67169 | 58227 | 325 | 0.06 | 0.02 | 8.28 | 8.18 | 0.01 | 0.97 |
| P6 | sferico | 16.4 | 53918 | 48793 | 342 | 26.71 | 0.07 | 5.39 | 5.07 | 0 | 1.06 |
| P7 | sferico | 6.5 | 68249 | 65630 | 7 | 20.34 | 0.02 | 3.77 | 3.37 | 0 | 1.1 |
| P8 | sferico | 10.4 | 67467 | 60833 | 337 | 33.46 | 0.04 | 4.19 | 4.34 | 0 | 0.97 |
| P9 | sferico | 0 | 60439 | 52415 | 326 | 0.07 | 0.06 | 8.34 | 8.15 | 0.02 | 1.06 |
| P10 | sferico | 0 | 67098 | 58255 | 316 | 0.09 | -0.05 | 12.7 | 12.18 | 0.01 | 0.98 |
| P11 | circolare | 0 | 60365 | 47364 | 312 | 0.09 | -0.03 | 20.4 | 18.41 | 0.01 | 0.99 |
| P12 | sferico | 0 | 60413 | 52416 | 313 | 0.11 | 0.16 | 26.7 | 21.42 | 0.02 | 1.01 |
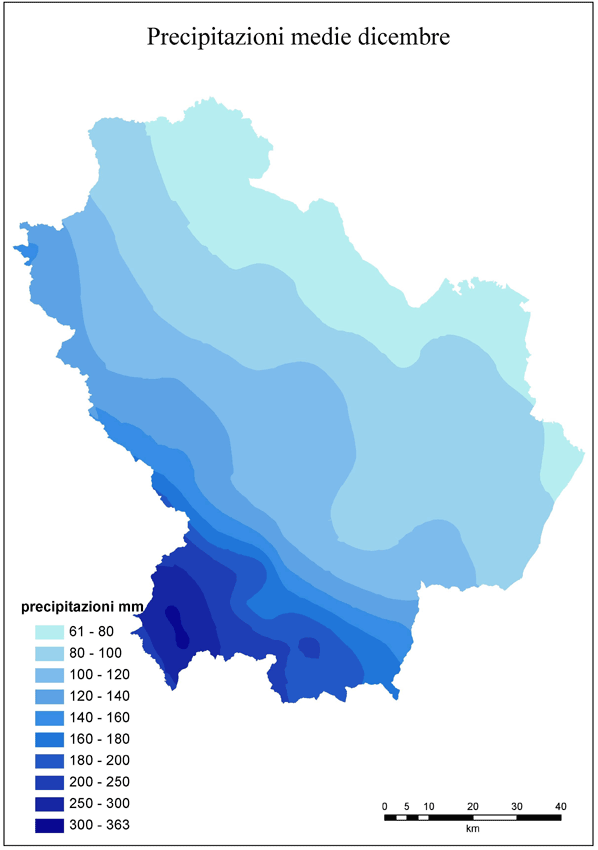
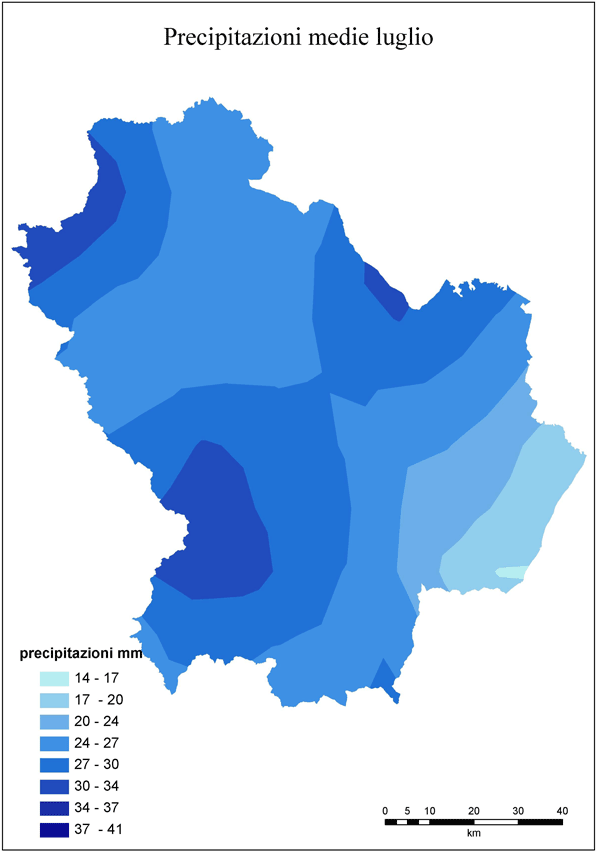
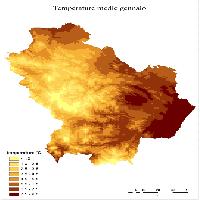
Come esempio delle mappe finali prodotte sono rappresentate in Fig. 3 e Fig. 4 le precipitazioni medie di dicembre (mese più piovoso) e di luglio (mese più secco).
Per l’interpolazione delle temperature, tenuto conto della natura della variabile, della numerosità delle stazioni e della distribuzione spaziale delle stesse, è stata adottata la metodologia di seguito brevemente riassunta ([30]). La stretta correlazione tra i dati termici e altitudine viene espressa in fisica come lapse-rate ([34]), che indica l’abbassamento di temperatura in gradi centigradi per incremento unitario della quota. Il lapse-rate è calcolato, tramite regressione tra altitudine e temperatura delle diverse stazioni (Tab. 4). Le temperature delle stazioni sono riportate a livello del mare (eqn. 4):
dove t0 è la temperatura a livello del mare, α è il lapse-rate e m è la quota della stazione. Le temperature t 0 sono poi interpolate con RST. Successivamente le superfici create vengono riportate alla quota effettiva con un procedimento inverso al precedente utilizzando un modello digitale del terreno (eqn. 5):
dove ti sono le temperature interpolate a livello del mare, DEM è il modello di elevazione digitale del terreno e α è il lapse-rate L’applicazione di tale metodo ha portato quindi alla produzione di mappe relative alle temperature medie mensili.
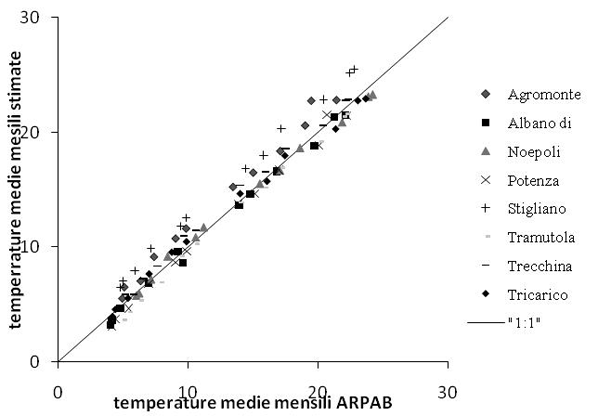
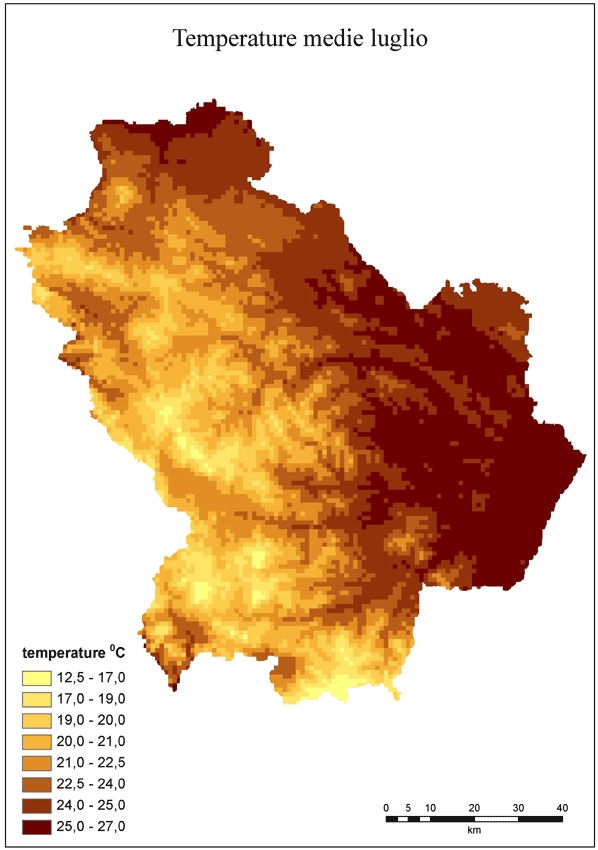
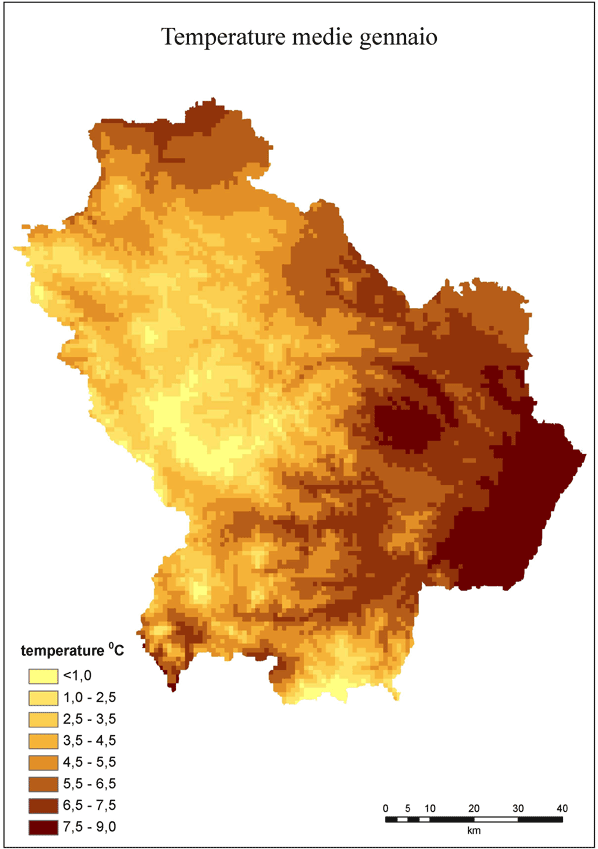
I valori interpolati sono stati confrontati con le temperature medie di 8 stazioni afferenti alla rete ARPAB. Queste erano infatti le sole stazioni termometriche che non coincidevano con quelle della rete ALSIA usata per l’interpolazione. In questo caso entrambi i dataset sono stati ottenuti mediando i valori sul periodo 1996-2006. I risultati del confronto sono riportati nella Tab. 7 e nella Fig. 5 sotto forma grafica. È evidente il buon adattamento tra dati interpolati e misurati con R2 prossimi a uno e con la nuvola di punti compatta intorno alla linea 1:1. L’errore (RMSE) va da 0.5 a 1.3°C, con un errore percentuale che non supera l’8%. Stigliano che ha la quota più bassa, ha anche l’errore più elevato. Questo potrebbe indicare la tendenza del metodo a sovrastimare i valori per le stazioni dislocate a quote relativamente basse. La pendenza prossima a uno e l’intercetta confermano che la stima è poco distorta. Nelle Fig. 6 e Fig. 7 ci sono le mappe di luglio e gennaio dalle quali, a differenza di quelle ottenute con il kriging, è evidente l’effetto pixel dovuto all’uso del DEM per la produzione delle mappe finali.
Tab. 7 - Confronto tra le temperature interpolate e misurate. Le coordinate sono in UTM WGS 84 33N. (ns): p>0.05 - non significativo; (*): p<0.05 - significativo; (**): p<0.01 - altamente significativo.
| Stazione | E (m) |
N (m) |
quota (m) |
Analisi di Regressione lineare | ||||
|---|---|---|---|---|---|---|---|---|
| Slope | Intercetta (°C) |
R2 | RMSE (°C mese-1) |
RMSE % |
||||
| Agromonte | 589452 | 4435758 | 493 | 1.05 | 0.98** | 0.99 | 0.51 | 3.49 |
| Albano | 587666 | 4492870 | 827 | 1.00 | 0.31** | 0.99 | 0.52 | 3.00 |
| Noepoli | 613373 | 4438556 | 627 | 0.94 | 0.55ns | 0.99 | 0.53 | 2.93 |
| Potenza | 567828 | 4498770 | 799 | 1.02 | 0.69** | 0.99 | 0.61 | 3.64 |
| Stigliano | 613226 | 4472454 | 270 | 1.99 | 0.99** | 0.99 | 1.35 | 7.76 |
| Tramutola | 565753 | 4464147 | 657 | 1.02 | 0.95** | 0.99 | 0.78 | 4.32 |
| Trecchina | 566831 | 4429974 | 412 | 0.99 | 0.75* | 0.99 | 0.84 | 5.22 |
| Tricarico | 597160 | 4496916 | 674 | 0.95 | 0.67ns | 0.99 | 0.67 | 3.63 |
Fig. 5 - Confronto tra temperature interpolate e temperature misurate da 8 stazioni afferenti alla rete ARPAB.
Si può in definitiva affermare che l’interpolazione delle temperature medie mensili ottenuta con la tecnica in precedenza descritta ha sicuramente restituito un buon risultato soprattutto considerando l’esiguo numero di stazioni termometriche, la loro dislocazione spaziale e le condizioni morfo-topografiche complesse della Basilicata.
Discussione
Il problema principale nell’interpolazione delle variabili climatiche della Basilicata è dato dalla mancanza di una buona base di dati. Il numero delle stazioni termometriche, in particolare, non è sufficiente, con una copertura media di una stazione maggiore di 330 km2. Le stesse non sono inoltre distribuite in maniera omogenea lungo il profilo altitudinale: la fascia compresa tra i 700 e i 1000 metri è rappresentata da sole 3 stazioni mentre non esistono stazioni comprese tra 1000 e 2400 metri. L’area nord occidentale ne è quasi priva per cui le temperature interpolate in quell’area potrebbero non essere rappresentative dei valori reali. Considerando invece la natura degli eventi piovosi e la presenza di aree con regimi pluviometrici nettamente distinti, la rete di stazioni pluviometriche andrebbe infittita soprattutto nella zona sud-ovest dove le precipitazioni sono abbondanti. In questo modo la correlazione spaziale locale potrebbe essere definita in modo più preciso. Un altro problema è legato alla qualità dei dati grezzi: le registrazioni presentano interruzioni nelle acquisizioni che andrebbero colmate per ricostruire, in maniera definitiva, l’intera serie storica ([1]).
Per quanto riguarda i metodi d’interpolazione vi è da sottolineare che per le precipitazioni sono diversi i lavori che propongono di usare l’altitudine come variabile accessoria nelle interpolazioni per ottenere stime più precise ([22]). Generalmente le precipitazioni, nelle regioni montuose, tendono ad aumentare con l’altitudine, principalmente a causa dell’effetto orografico che costringe le correnti di aria a risalire verticalmente e a condensarsi per il raffreddamento adiabatico ([19]). Uno degli approcci più conosciuti è quello di Daly et al. ([12]) che stima le precipitazioni per ogni cella del DEM utilizzando la regressione della pioggia con l’altitudine. A questa metodologia se ne sono affiancate altre più complesse e di tipo geostatistico ([19], [24], [21]). Nella presente area di studio questa relazione non è stata rinvenuta per cui i metodi sopra citati non sono stati tenuti in considerazione.
Claps & Mancino ([8]) in uno studio sulla Basilicata hanno individuato una relazione lineare tra le precipitazioni, l’altitudine e la distanza delle stazioni dalla linea di costa. Per la Basilicata, inoltre, il kriging si è già dimostrato un metodo adatto per l’interpolazione dei dati pluviometrici ([31]).
Per quanto riguarda le temperature, la relazione molto significativa tra il dato termico e l’altitudine, già in precedenza rinvenuta per l’area in esame ([6], [8]), ha fornito una valida informazione aggiuntiva, soprattutto considerando l’esiguo numero di stazioni termometriche, consentendo l’applicazione di un metodo d’interpolazione in fasi differenti, di cui una è in ogni caso rappresentata da un’operazione di interpolazione non regressiva. I modelli regressivi puri, infatti, presentano il limite di considerare ogni singola cella in maniera isolata senza fare riferimento alla continuità spaziale delle variabili climatiche. La metodologia adottata in questa ricerca può essere considerata un buon compromesso tra i due differenti metodi e si è dimostrata in grado, come ha confermato il confronto con un dataset indipendente, di restituire buoni risultati.
Conclusioni
Usando due diverse tecniche di interpolazione sono stati realizzati strati informativi relativi alla piovosità mensile e alle temperature medie mensili della Basilicata. Per le precipitazioni l’UK si è dimostrato essere in grado di minimizzare gli errori di stima delle superfici. Le temperature sono invece state interpolate seguendo un approccio che sfrutta il lapse-rate per ottenere risultati più precisi in aree a morfologia complessa e laddove la numerosità campionaria risulta carente e la dislocazione delle stazioni non in grado di rappresentare l’intera variabilità altitudinale. I risultati consentono di affermare che le mappe ottenute sono in grado di interpretare la variabilità spaziale dei fenomeni indagati. Gli strati informativi ottenuti possono, dunque, essere utilizzati come dati di input all’interno di modelli che prevedano l’utilizzo di informazioni climatiche spazializzate.
Ringraziamenti
Si ringraziano il dr. Angelo Nolè, il dr. Scalcione dell’ALSIA e il prof. Nick Chappell dell’Università di Lancaster, Regno Unito.
References
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
Online | Google Scholar
Google Scholar
Online | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Online | Google Scholar
Online | Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar