Forest canopy analysis in the Alpine environment: comparison among assessment methods
Forest@ - Journal of Silviculture and Forest Ecology, Volume 10, Pages 43-54 (2013)
doi: https://doi.org/10.3832/efor0974-010
Published: Apr 15, 2013 - Copyright © 2013 SISEF
Research Articles
Abstract
Forest canopy analysis in the Alpine environment: comparison among assessment methods. Forest canopy is an important ecological feature of forest stands and can be expressed as Leaf Area Index (LAI) or canopy cover percentage. LAI is the ratio between leaf area and ground area (m2 m-2) and it can be measured using an angle of 180°. Instead, the canopy cover is the percentage of forest area occupied by the vertical projection of tree crowns; consequently, LAI expresses the canopy closure rather than the canopy cover. This paper focuses on the estimation of LAI and canopy cover percentage in 54 sampling points randomly distributed over the main forest types of Trentino (beech forests, Scots pine forests, Norway spruce forests and European larch forests). The main purpose was the analysis of relationship between LAI and canopy cover percentage, the latter measured with two different techniques: visual estimation and estimation using the spherical densiometer. In the last part of the paper, LAI data collected in the four main forest types of Trentino are compared with values reported in the literature for the same forest types.
Keywords
Leaf Area Index (LAI), Canopy Cover, Hemispherical Images, Visual Estimation, Spherical Densiometer, Trentino
Introduzione
L’indice di area fogliare (Leaf Area Index o LAI) e il grado di copertura (canopy cover percentage) sono due espressioni della copertura forestale che assumono una notevole rilevanza nella definizione dei modelli di sviluppo delle formazioni arboree e dell’analisi dei processi ecologici ([25]). La distribuzione della luce sotto la copertura arborea è strettamente dipendente dal LAI e dal grado di copertura di un popolamento forestale e influenza la numerosità ([46]) e la distribuzione della rinnovazione ([52]). Secondo quanto dimostrato da Machado & Reich ([44]), il LAI spiega il 90% della variazione giornaliera del flusso di fotoni, pertanto, il suo studio appare come un metodo efficiente per la stima della capacità di tolleranza all’ombra degli individui che crescono sotto copertura. Inoltre, l’accurata misura della copertura forestale è di cruciale importanza per studi e ricerche in vari ambiti disciplinari quali l’idrologia, la selvicoltura, gli inventari forestali e il monitoraggio ambientale ([16], [51], [12]).
LAI e grado di copertura sono due caratteristiche misurate sulla canopy di un popolamento arboreo. Tuttavia, mentre il grado di copertura è misurato secondo la proiezione verticale delle chiome ed esprime la canopy cover, il LAI è misurato su un angolo di 180° con il vertice rivolto verso il basso ed esprime la canopy closure ([35]). In altre parole, la canopy closure rappresenta la porzione di cielo, osservata con uno strumento emisferico da un punto posto al di sotto delle chiome, che viene oscurata dalla vegetazione ([26]). Nello specifico, i metodi che stimano il LAI si dividono in metodi basati su misure multiple simultanee della trasmittanza (LAI-2000 e foto emisferiche) e metodi basati su misure singole (Ceptometer e foto ad angoli ristretti). A partire dalla misura della canopy cover è comunque possibile calcolare il LAI impiegando la legge di Beer-Lambert che correla la quantità di luce assorbita da un mezzo attraversato (copertura fogliare) alle caratteristiche del mezzo stesso quali la concentrazione e lo spessore ([45], [13]).
Il LAI è un indice che esprime l’area fogliare di un ecosistema ([42]) ed è dato dal rapporto tra la superficie occupata dalle chiome rispetto a una superficie di riferimento (m2 m-2 - [10]). Tale indice dinamico esprime la superficie fotosintetica e di traspirazione delle coperture forestali ([27]) e dipende da vari fattori ambientali (climatici e di disponibilità idrica - [8]). In considerazione di questo fatto, il LAI può assumere un ampio range di valori in funzione della formazione vegetale analizzata ([5]) e, nell’ambito della stessa formazione, in relazione alla disponibilità di risorse e allo stadio di sviluppo. Il LAI controlla, in maniera diretta o indiretta, una moltitudine di processi biologici, fisici e biogeochimici nei cicli dell’acqua, del carbonio e di varie sostanze nutritive ([20]). In particolare, la densità fogliare delle chiome influenza la produzione primaria (fotosintesi), la traspirazione, il grado d’intercettazione delle precipitazioni e lo scambio di energia tra la vegetazione e l’atmosfera ([41]).
In letteratura si riscontra una moltitudine di metodi per la stima del LAI ([4]), classificabili principalmente in metodi diretti e metodi indiretti. I primi misurano le dimensioni delle foglie in maniera diretta e possono essere distruttivi (misura diretta su campioni prelevati dalle chiome) o non distruttivi (misure sulla lettiera), richiedono un gran dispendio di energie e sono più appropriati per formazioni erbacee o arbustive. I metodi indiretti utilizzano parametri (misure allometriche, trasmittanza) che possono essere misurati in maniera più speditiva ([42]), sono più idonei per misure in formazioni arboree e si dividono in metodi indiretti “di contatto” (misure allometriche, plumb lines e inclined point quadrats) e metodi indiretti di tipo ottico (Ceptometer, fotografie emisferiche, LAI-2000, TRAC, DEMON e undirectional view digital photography - [37], [49], [43]).
L’uso delle fotografie emisferiche per la stima dei valori di LAI è stato applicato per la prima volta da Anderson ([2]) ed è divenuto di uso comune in seguito allo sviluppo e alla diffusione di fotocamere digitali che hanno ridotto i tempi di acquisizione ed elaborazione delle immagini ([61]). La tecnica è largamente applicata in studi di tipo ecologico sulla luce e sul regime luminoso, sull’acqua, sull’insediamento e l’affermazione della rinnovazione, per la stima delle caratteristiche allometriche, per l’analisi degli effetti dei diradamenti, come indicatore della salute dei soprassuoli forestali e nello sviluppo di modelli previsionali.
Il grado di copertura, detto anche site factor ([2]), è definito in letteratura come la frazione di suolo coperta dalla proiezione verticale delle chiome degli alberi, ed è comunemente espresso in forma di percentuale (canopy cover percentage o, il suo inverso, canopy openness percentage). In Italia, nella normale pratica inventariale e assestamentale, il grado di copertura viene generalmente stimato a vista impiegando classi percentuali più o meno ampie. Nonostante questa consuetudine dettata da motivazioni economiche, il grado di copertura può essere misurato anche mediante l’utilizzo di strumenti che forniscono un valore meno soggettivo quali il tubo di Cajanus o i densiometri ([56]), l’analisi d’immagini satellitari ([35]), l’applicazione di modelli probabilistici ([36]) e il LAI-2000 ([56]).
A partire da queste considerazioni, il presente contributo si è focalizzato sullo studio del LAI e del grado di copertura dei principali tipi forestali del Trentino (faggete, pinete di pino silvestre, peccete e lariceti). Il principale obiettivo della ricerca è stato il confronto tra LAI e grado di copertura. Quest’ultimo è stato misurato con due differenti procedure: stima a vista e attraverso l’impiego del densiometro sferico. L’impiego di due differenti procedure si è reso necessario in quanto la stima a vista fornisce un risultato per la canopy cover, mentre il densiometro sferico stima la canopy closure impiegando un angolo di 60°. Nell’ultima parte del lavoro si è proceduto con la comparazione dei valori di LAI con i valori riportati in letteratura per gli stessi tipi forestali. Nel presente lavoro, così come nella letteratura internazionale, il termine LAI è stato utilizzato in sostituzione del più consono termine PAI (Plant Area Index).
Materiali e metodi
Area di studio
L’area di studio è la provincia di Trento il cui territorio è quasi esclusivamente montano (soltanto poco meno del 10% del territorio provinciale è posto al di sotto dei 500 m s.l.m.) e comprende dieci cime che superano i 3000 m. Dal punto di vista geologico la provincia di Trento è molto eterogenea ed è stata modellata dai fenomeni esogeni tipici dell’area Alpina, di cui le valli glaciali sono la massima testimonianza. I principali tipi di rocce che ne caratterizzano la litografia rientrano tra le rocce metamorfiche (in particolare scisti), le rocce vulcaniche (graniti, dioriti, porfidi), e le rocce sedimentarie (calcari e dolomie - [7]).
Nella provincia di Trento il clima è di tipo temperato-continentale con alcune significative differenze tra le valli orientali, quelle occidentali e il fondovalle. Nella valle dell’Adige la temperatura media annua è di 11.5 °C con una pluviometria media annua di 883 mm caratterizzata da un picco primaverile (94 mm di pluviometria media nel mese di maggio) e uno autunnale (110 mm di pluviometria media nel mese di ottobre). Dal punto di vista bioclimatico il Trentino rientra in prevalenza nelle categorie sovratemperato umido e orotemperato umido secondo la classificazione di Rivas-Martinez (Tab. 1).
Tab. 1 - Classificazioni climatiche e bioclimatiche nel territorio della Provincia di Trento e numero di aree di saggio (AdS) ricadenti in ciascun classe. WBCS (World wide Bioclimatic Classification System). Fonte: modificato da Sboarina & Cescatti ([58]).
| Indice | Classi [% del territorio provinciale] |
Numero AdS | |
|---|---|---|---|
| Corrispondenza tra pluviofattore di Lang e classificazione fitoclimatica di Pavari | Lauretum (13.1) | 3 | |
| Castanetum (26.2) | 15 | ||
| Fagetum (20.5) | 15 | ||
| Picetum (36.3) | 21 | ||
| assenza di humus (3.9) | - | ||
| Indice igrotermico di Amann | oceanico temperato (35.4) | 9 | |
| continentale (20.3) | 3 | ||
| intermedio (44.3) | 42 | ||
| Indice di continentalità pluviale di Angot | alpico (90.5) | 50 | |
| endoalpico (9.5) | 4 | ||
| WBCS di RivasMartinez | Indice di continentalità | temperato oceanico (98.4) | 51 |
| temperato continentale (1.6) | 3 | ||
| Indice di termicità | sovra temperato (27.6) | 9 | |
| mesotemperato (72.4) | 45 | ||
| Indice ombrotermico | subumido (0.3) | - | |
| umido (95.1) | 49 | ||
| iperumido (4.6) | 5 | ||
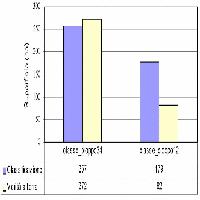
In Trentino l’indice di boscosità, secondo i dati dell’Inventario Nazionale delle Foreste e dei serbatoi forestali di Carbonio (INFC), corrisponde a circa il 60% dell’intero territorio provinciale (372 879 ha). I principali tipi forestali presenti in provincia di Trento sono le peccete pure o miste ad abete bianco (Abies alba Mill., 41.0%), i lariceti puri e misti con pino cembro (Pinus cembra L., 16.9%), le faggete (16.7%) e le pinete di pino silvestre (Pinus sylvestris L., 5.7% - [17]). Il 75% dei boschi provinciali è soggetto ad un piano di gestione: risultano assestate tutte le proprietà pubbliche, appartenenti prevalentemente ai comuni e al demanio provinciale, nonché le proprietà collettive (Magnifica Comunità della Val di Fiemme, Regole Spinale-Manez, Consortele della Val di Rabbi, Amministrazioni Separate per il Beni di Uso Civico, ecc.) e le grandi proprietà private. Al contrario la proprietà privata di piccole e medie dimensioni, che corrisponde a poco più del 20% dell’area forestale totale, non risulta, invece, soggetta a piano di gestione, ma è periodicamente inventariata e monitorata dal Servizio Foreste della Provincia Autonoma di Trento (PAT).
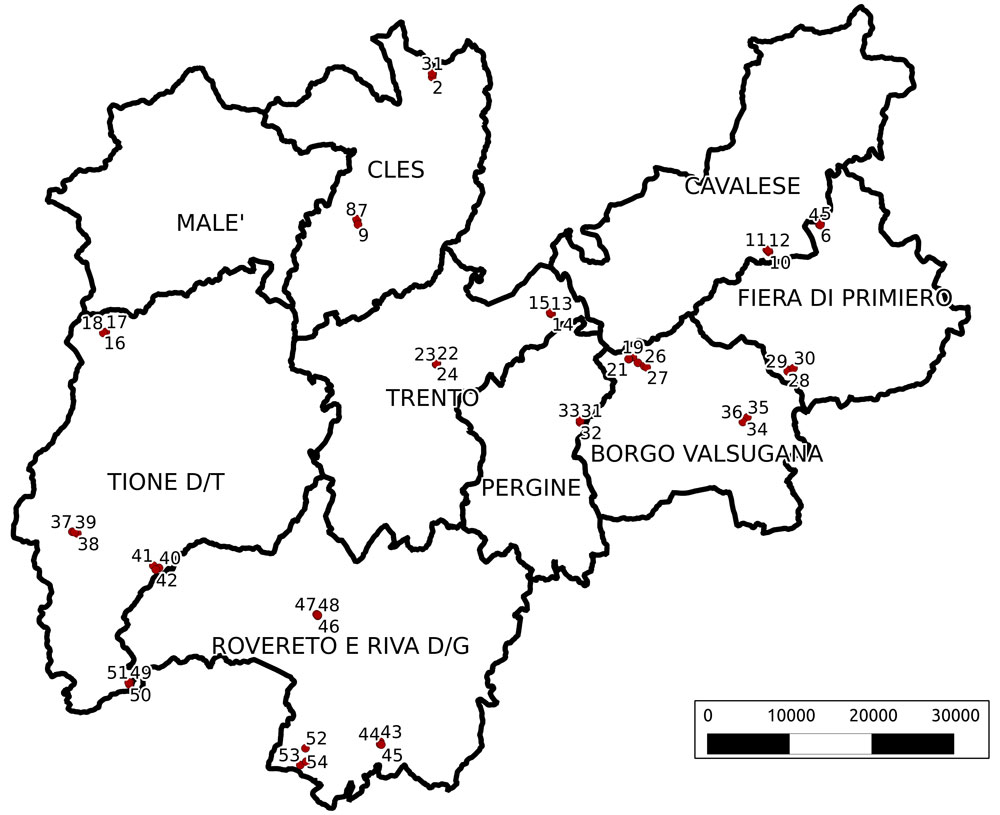
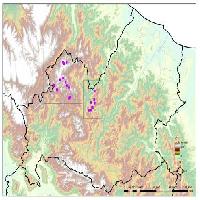
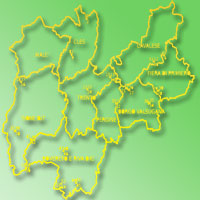
Lo studio è stato condotto in 54 punti di campionamento estratti in maniera casuale all’interno delle quattro principali categorie della carta dei tipi forestali redatta dalla Provincia di Trento (faggete, pinete di pino silvestre, peccete e lariceti - Fig. 1). Al fine di semplificare l’analisi dal punto di vista statistico le formazioni ad abete bianco, anche per via delle proprie caratteristiche ecologiche e strutturali, sono state considerate congiuntamente alle peccete. Le unità di campionamento impiegate sono state, in analogia con quelle impiegate dall’INFC, delle aree di saggio circolari di 13 m di raggio (532 m2). La selezione dei centri delle aree di saggio è stata effettuata in ambiente GIS (Quantum-GIS) secondo due fasi: nella prima fase, a partire dalla carta dei tipi forestali sono stati estratti casualmente 18 poligoni con superficie maggiore a 10 ha stratificando per tipo forestale. Successivamente, al loro interno, sono state estratte le coordinate dei centri delle aree di saggio in numero di 3 per ciascun poligono (54 aree di saggio). Le aree di saggio sono risultate così ripartite per tipo forestale: 21 in peccete e abetine (44.5%), 12 in faggete (22.2%), 12 in pinete (22.2%) e 6 in lariceti (11.1%). Suddette aree di saggio sono distribuite in un ampio intervallo altitudinale (410-1963 m s.l.m.) e con pendenze medie comprese tra 0° e 40° (Tab. 2). Tale ripartizione delle 54 aree di saggio ci consente di ipotizzare che il campione selezionato ben rappresenti la variabilità altitudinale e morfologica dei tipi forestali presenti in provincia di Trento.
Fig. 1 - Distribuzione dei punti di campionamento all’interno del territorio della provincia di Trento ripartiti per distretti forestali.
Tab. 2 - Principali informazioni dendrometriche e strutturali delle 54 aree di saggio (AdS).
| Tipo forestale | AdS | Alberi (n ha-1) |
Area basimetrica (m2 ha-1) |
Altitudine (m s.l.m.) |
TM | R | x | y |
|---|---|---|---|---|---|---|---|---|
| Faggeta | 22 | 2469 | 36.4 | 540 | 0.42 | 0.99 | 66°40’06’’ | 51°13’707’’ |
| 23 | 773 | 30.9 | 536 | 0.5 | 1.66 | 66°38’72’’ | 51°13’555’’ | |
| 24 | 1244 | 45.2 | 553 | 0.4 | 1.44 | 66°39’17’’ | 51°13’636’’ | |
| 40 | 565 | 21.3 | 410 | 0.49 | 1.39 | 65°70’87’’ | 50°67’651’’ | |
| 41 | 1847 | 20 | 543 | 0.43 | 1.51 | 65°70’86’’ | 50°67’353’’ | |
| 42 | 867 | 25.8 | 488 | 0.48 | 1.58 | 65°72’66’’ | 50°67’313’’ | |
| 46 | 565 | 21.3 | 1209 | 0.49 | 1.39 | 64°80’06’’ | 50°66’873’’ | |
| 47 | 565 | 24.5 | 1408 | 0.39 | 1.69 | 64°80’04’’ | 50°66’856’’ | |
| 48 | 735 | 30.3 | 1386 | 0.29 | 1.55 | 64°77’25’’ | 50°65’469’’ | |
| 52 | 1055 | 36.4 | 132 | 0.52 | 1.59 | 62°47’08’’ | 50°75’391’’ | |
| 53 | 660 | 21.6 | 1281 | 0.42 | 1.54 | 62°48’89’’ | 50°75’489’’ | |
| 54 | 2073 | 43.9 | 1235 | 0.41 | 1.33 | 62°50’70’’ | 50°75’709’’ | |
| - | 1118.2 | 28.5 | - | 0.44 | 1.47 | - | - | |
| Lariceto | 16 | 773 | 85.6 | 1602 | 0.5 | 1.27 | 62°34’71’’ | 51°17’396’’ |
| 17 | 433 | 71.9 | 1632 | 0.31 | 1.01 | 62°33’91’’ | 51°17’132’’ | |
| 18 | 433 | 81.1 | 1679 | 0.18 | 1.06 | 62°29’31’’ | 51°17’134’’ | |
| 31 | 113 | 42.1 | 1888 | 0.45 | 1.64 | 68°14’65’’ | 51°06’681’’ | |
| 32 | 641 | 36.3 | 1864 | 0.49 | 1.66 | 68°13’91’’ | 51°06’484’’ | |
| 33 | 377 | 37 | 1862 | 0.26 | 1.83 | 68°13’89’’ | 51°06’725’’ | |
| - | 461.7 | 59.0 | - | 0.36 | 1.41 | - | - | |
| Pecceta | 4 | 716 | 55.6 | 1549 | 0.42 | 1.67 | 71°08’76’’ | 51°31’310’’ |
| 5 | 1168 | 75.2 | 1538 | 0.49 | 0.98 | 71°09’36’’ | 51°31’234’’ | |
| 6 | 1018 | 61.5 | 1568 | 0.5 | 1.32 | 71°10’37’’ | 51°31’192’’ | |
| 10 | 754 | 47.4 | 1901 | 0.52 | 1.12 | 70°41’18’’ | 51°27’537’’ | |
| 11 | 829 | 51.7 | 1894 | 0.44 | 1.19 | 70°41’10’’ | 51°27’493’’ | |
| 12 | 490 | 38.5 | 1963 | 0.53 | 1.01 | 70°42’66’’ | 51°27’486’’ | |
| 19 | 1168 | 45.1 | 1594 | 0.47 | 0.96 | 68°78’15’’ | 51°14’420’’ | |
| 20 | 396 | 41.2 | 1592 | 0.28 | 1.17 | 68°73’26’’ | 51°14’177’’ | |
| 21 | 1074 | 56.2 | 1601 | 0.41 | 1.15 | 68°72’83’’ | 51°14’197’’ | |
| 25 | 490 | 60.1 | 1413 | 0.21 | 1.7 | 68°85’62’’ | 51°13’713’’ | |
| 26 | 377 | 56.6 | 1476 | 0.45 | 1.61 | 68°92’01’’ | 51°13’346’’ | |
| 27 | 471 | 63.7 | 1479 | 0.45 | 1.87 | 68°94’93’’ | 51°13’175’’ | |
| 28 | 1018 | 73.1 | 1490 | 0.46 | 1.61 | 70°72’86’’ | 51°12’890’’ | |
| 29 | 1112 | 55.5 | 1470 | 0.48 | 1.64 | 70°66’33’’ | 51°12’698’’ | |
| 30 | 565 | 36 | 1610 | 0.61 | 1.59 | 70°73’37’’ | 51°13’086’’ | |
| 34 | 1545 | 37.8 | 1460 | 0.41 | 1.4 | 70°15’81’’ | 51°06’954’’ | |
| 35 | 1734 | 58.3 | 1410 | 0.32 | 1.53 | 70°17’25’’ | 51°07’102’’ | |
| 36 | 791 | 37.9 | 1552 | 0.56 | 1.57 | 70°11’69’’ | 51°06’544’’ | |
| 37 | 810 | 68.2 | 1453 | 0.49 | 1.78 | 63°00’84’’ | 50°88’760’’ | |
| 38 | 1112 | 40.2 | 1327 | 0.38 | 1.48 | 62°95’60’’ | 50°89’105’’ | |
| 39 | 471 | 54.4 | 1634 | 0.46 | 1.50 | 62°98’05’’ | 50°88’576’’ | |
| 49 | 829 | 73.3 | 1707 | 0.45 | 1.72 | 61°69’06’’ | 50°99’906’’ | |
| 50 | 1206 | 47.7 | 1715 | 0.44 | 1.55 | 71°45’70’’ | 51°53’588’’ | |
| 51 | 848 | 53.5 | 1771 | 0.39 | 1.49 | 61°67’09’’ | 51°00’411’’ | |
| - | 874.7 | 53.7 | - | 0.44 | 1.44 | - | - | |
| Pineta | 1 | 1734 | 40.9 | 1137 | 0.25 | 1.12 | 66°35’55’’ | 51°48’128’’ |
| 2 | 2544 | 44.8 | 1195 | 0.36 | 1.15 | 66°34’25’’ | 51°48’478’’ | |
| 3 | 622 | 38.3 | 1129 | 0.27 | 0.98 | 66°33’44’’ | 51°48’030’’ | |
| 7 | 2751 | 45.7 | 997 | 0.45 | 0.9 | 65°42’76’’ | 51°31’093’’ | |
| 8 | 2601 | 41.6 | 952 | 0.39 | 0.94 | 65°42’78’’ | 51°31’239’’ | |
| 9 | 2638 | 37 | 924 | 0.4 | 0.95 | 65°44’92’’ | 51°30’468’’ | |
| 13 | 1545 | 50.6 | 924 | 0.42 | 0.81 | 67°78’02’’ | 51°19’711’’ | |
| 14 | 1545 | 38.4 | 924 | 0.4 | 1.03 | 67°79’24’’ | 51°19’685’’ | |
| 15 | 1281 | 48.8 | 924 | 0.44 | 1.03 | 67°77’49’’ | 51°19’831’’ | |
| 43 | 2148 | 30.9 | 1070 | 0.42 | 1.47 | 64°94’98’’ | 50°82’966’’ | |
| 44 | 1715 | 40.4 | 1090 | 0.51 | 1.49 | 64°94’09’’ | 50°83’111’’ | |
| 45 | 3467 | 34.4 | 1085 | 0.35 | 1.18 | 64°95’02’’ | 50°83’055’’ | |
| - | 2049.3 | 69.7 | - | 0.39 | 1.09 | - | - |
La densità delle formazioni analizzate è risultata piuttosto variabile con un numero di piante ad ettaro compreso tra un minimo di 377 e un massimo di 3467. Nello specifico le pinete di pino silvestre sono risultate le formazioni con il più alto numero medio di soggetti a ettaro (2049 piante ha-1) mentre i lariceti quelli con il minor numero medio di soggetti ad ettaro (462 piante ha-1). In termini di area basimetrica si riscontrano valori medi di circa 70 m2 ha-1 per le pinete di pino silvestre e di circa 60 m2 ha-1 per i lariceti, mentre valori piuttosto bassi si sono riscontrati per le faggete (28.5 m2 ha-1). Il numero di specie rilevato in ciascun’area di saggio è risultato variabile da un minimo di una sola specie, in particolare nelle peccete, ad un massimo di nove specie.
All’interno di ciascun’area di saggio (AdS), su tutti i soggetti arborei con diametro a petto d’uomo superiore a 4.5 cm è stata rilevata la specie e sono stati effettuati tre tipi di misure: (1) di posizione (distanza e azimut relativi calcolati rispetto al centro dell’area di saggio); (2) dendrometriche (diametro a petto d’uomo); e (3) di copertura (grado di copertura espresso in percentuale e stima del LAI attraverso l’impiego delle foto emisferiche).
Struttura orizzontale
Le misure di posizione e dendrometriche sono state impiegate per analizzare la struttura orizzontale dei popolamenti forestali oggetto di analisi, quest’ultima utilizzata quale espressione della distribuzione delle piante nello spazio e della loro differenziazione diametrica ([53]). La scelta di dare particolare enfasi alla stima della struttura orizzontale del popolamento è stata dettata dallo stretto legame tra questa caratteristica e la copertura forestale ([60]). La struttura orizzontale è stata misurata attraverso l’impiego di due indici sintetici: l’indice di differenziazione diametrica e l’indice di aggregazione di Clark-Evans.
L’indice di differenziazione diametrica (TM), così come elaborato da Füldner ([22]), prende in considerazione la distribuzione dei diametri all’interno dell’area di saggio e può assumere valori tra 0 e 1. Valori dell’indice inferiori a 0.3 indicano una bassa differenziazione diametrica, mentre valori superiori a 0.8 indicano un’elevata differenziazione diametrica (eqn. 1):
dove TM è l’indice di differenziazione diametrica; n è il numero di alberi interni all’area di saggio con diametro superiore a 4.5 cm a petto d’uomo; dij è il rapporto tra il diametro a petto d’uomo più piccolo e quello più grosso tra l’albero i e i suoi tre più prossimi vicini.
L’indice di aggregazione di Clark & Evans ([14]) fornisce un valore sintetico della struttura orizzontale di un popolamento forestale sulla base della distanza tra alberi. Tale indice (R) può assumere valori compresi tra 0 e 2.1491. Secondo gli autori i valori inferiori a 0.86 sono indicativi di una struttura a cluster, mentre valori superiori a 1.29 indicano una struttura regolare. Valori compresi tra queste due soglie, invece, indicano una distribuzione randomizzata degli alberi. L’indice di aggregazione di Clark-Evans può essere così espresso dal punto di vista matematico (eqn. 2):
dove R è l’indice di aggregazione di Clark-Evans; n è il numero di alberi interni all’area di saggio con diametro superiore a 4.5 cm a petto d’uomo; r è la distanza dell’albero i dal suo più prossimo vicino (m); Pl è la dimensione dell’area di saggio (m2).
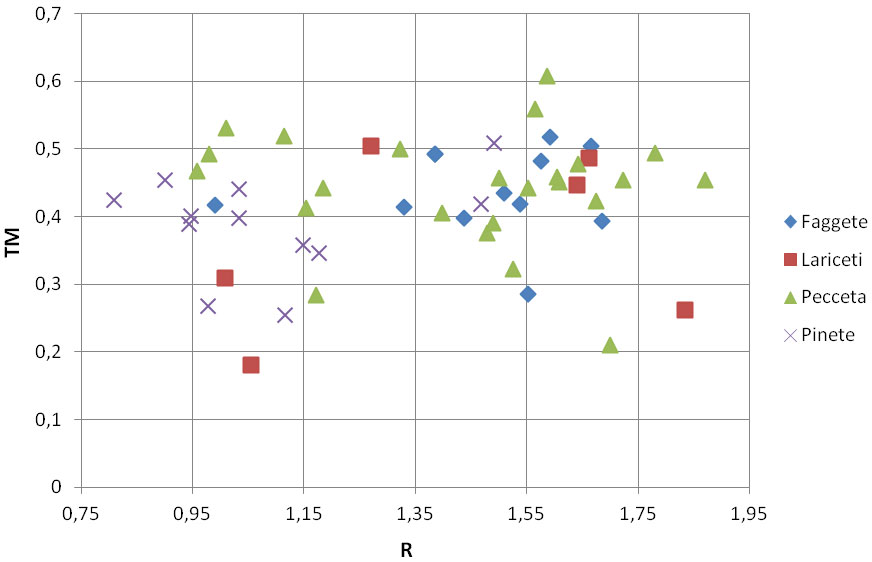
I boschi oggetto d’indagine mostrano dal punto di vista strutturale (Tab. 2) un’ampia diversità ai cui estremi si posizionano i cedui plurispecifici sotto fustaia di pino silvestre e le fustaie monospecifiche e monoplane principalmente ad abete rosso. Osservando i risultati medi riferiti ai due indici strutturali impiegati ci si rende conto che le faggete e le peccete del campione analizzato presentano una struttura analoga (TMpeccete=0.44, Rpeccete=1.44; TMfaggete=0.44, Rfaggete=1.47). Tuttavia le faggete mostrano una distribuzione più omogenea e risultano raggruppate nell’area del grafico con valori alti di R e di TM (Fig. 2). Al contrario le peccete sono separate in due gruppi con analoghi valori di TM, ma con valori di R maggiori e minori di 1.35 (rispettivamente strutture regolari e randomizzate). I valori più bassi in termini strutturali si riscontrano per le pinete di pino silvestre (TMpinete=0.39; Rpinete=1.09).
Fig. 2 - Dispersione dei 54 punti di campionamento sulla base dell’indice di aggregazione di Clark-Evans (R) e l’indice di differenziazione diametrica (TM).
Grado di copertura e LAI
Il grado di copertura è stato stimato sia a vista sia attraverso l’impiego di un densiometro sferico. La stima a vista del grado di copertura, per entrambi i metodi, è stata condotta da un unico operatore con pregressa esperienza nella valutazione delle coperture forestali. Nel presente lavoro, ai fini di un confronto con i dati raccolti con il densiometro sferico, è stato chiesto all’operatore di attribuire un valore medio di copertura dell’intera area di saggio, evitando l’impiego delle classi di copertura.
I densiometri sono strumenti che permettono di ottenere risultati attendibili sul grado di copertura in modo semplice e speditivo. Il densiometro sferico (Spherical Densiometer), impiegato nella presente ricerca, è stato sviluppato da Paul E. Lemmon e consiste in uno specchio concavo o convesso con sopra incisa una griglia di 24 quadrati all’interno dei quali si identificano 4 punti di osservazione. Per ciascuno dei 96 punti di osservazione totali l’operatore deve indicare se è coperto o meno dalle chiome degli alberi. Il numero totale dei punti coperti va successivamente moltiplicato per un coefficiente (1.04) al fine di ottenere la percentuale di copertura ([40]). Il densiometro sferico stima il grado di copertura impiegando un angolo di osservazione pari a 60°; conseguentemente è più corretto dire che tale strumento restituisce la canopy closure percentage anziché la canopy cover percentage. Si noti che al fine di stimare la canopy cover sarebbe necessario impiegare unicamente i 4 quadrati più prossimi all’operatore (16 punti di osservazione). La misura con densiometro sferico è stata eseguita dall’operatore posizionandosi a una distanza di 10 m dal centro dell’area di saggio in direzione dei quattro punti cardinali ed effettuando quattro misure in ciascun punto di osservazione. Il valore finale di copertura dell’intera area di saggio è stato calcolato come media delle sedici letture (quattro letture per ciascun punto di osservazione).
Inoltre, in corrispondenza del centro dell’area di saggio sono state scattate 4 fotografie emisferiche (una per ciascun punto cardinale) al fine di stimare il LAI. Le fotografie sono state scattate con una Nikon Coolpix 990 ed un Fish-eye converter Nikon FC-E8 (180° field of view) ponendo la fotocamera ad 1 m dal suolo e con la parte superiore in corrispondenza del punto cardinale prescelto. La fotocamera è stata utilizzata in modalità programme con esposizione e apertura automatici e parametri fissati sul programma FISHEYE1.
L’analisi delle fotografie emisferiche per la stima del LAI, in formato JPG e risoluzione 2048 x 1536 pixel, come consigliato da Frazer et al. ([21]), è stata effettuata mediante il software gratuito Spot Light Intercept Model (SLIM) 3.02a ([15]). Le operazioni di thresholding sono state eseguite in modalità automatica (Ridler clustering method), mentre la selezione della porzione d’immagine analizzata è stata effettuata manualmente.
L’esposizione è considerata una delle maggiori cause di errore nella stima del LAI ([11]). Come evidenziato da Chianucci & Cutini ([12]) la migliore esposizione per le fotografie emisferiche è quella in cui il cielo appare il più chiaro possibile tale da garantire il miglior contrasto tra le chiome e il cielo. Secondo suddetti autori il metodo più efficiente per ottenere tale risultato prevede di settare manualmente l’esposizione. Tuttavia, l’algoritmo di Ridler è molto robusto e minimizza gli effetti che il formato del file e la selezione della banda dell’immagine, che influenzano anche la scelta della migliore esposizione, hanno sulla stima dei parametri forestali ([55], [28]). Si ritiene, dunque, che l’applicazione dell’algoritmo di Ridler, accompagnato dall’esecuzione delle fasi di campionamento in giornate di cielo coperto ed in un limitato periodo dell’anno, possa minimizzare gli errori di stima causati dall’uso dell’esposizione automatica.
I valori di LAI e il grado di copertura stimato (a vista e con densiometro sferico) sono stati confrontati in termini statistici. Considerando che i dati di copertura non si distribuiscono in modo normale (test di Shapiro-Wilk: W=0.932, p=0.002; test di Anderson-Darling: A2=0.915, p=0.018), si è optato per l’impiego del test non-parametrico di Wilcoxon per evidenziare eventuali differenze statisticamente significative tra la stima del grado di copertura a vista e con densiometro sferico. Il test di correlazione di Spearman è stato utilizzato, invece, per analizzare la relazione esistente tra LAI e grado di copertura a vista e tra LAI e grado di copertura stimata con densiometro sferico.
Infine, i valori di LAI riscontrati in ciascuna tipologia sono stati confrontati con i riferimenti riportati in bibliografia per gli stessi tipi forestali. La ricerca è stata condotta utilizzando i dati raccolti nel database Global Leaf Area Index Data from Field Measurements, 1932-2000 ([57]) e integrati con quelli pubblicati in anni più recenti. La ricerca all’interno dei database è stata condotta sulla base della specie prevalente (dominant species) provvedendo successivamente a scremare la lista in considerazione della metodologia utilizzata.
Risultati e discussioni
I valori di LAI stimati attraverso l’elaborazione delle foto emisferiche sono compresi tra 1.16 e 4.76, mentre i valori di copertura forestale si distribuiscono in un intervallo tra 30% e 95% per la stima a vista e tra 67% e 96% per le misure con densiometro sferico. I valori medi per tipo forestale, con le rispettive deviazioni standard, sono illustrati nella Tab. 3. La prima differenza sostanziale riguarda la stima del grado di copertura a vista rispetto a quella rilevata attraverso l’impiego del densiometro sferico. Per tutti i tipi forestali il grado di copertura stimato a vista è inferiore a quello stimato con densiometro sferico, tali differenze si accentuano con il diminuire del grado di copertura e risultano massime nei lariceti, dove la differenza nella stima della copertura tra i due metodi è del 35%, e nelle peccete, dove tale differenza risulta di poco inferiore al 25%. La differenza risulta inferiore al 10% soltanto nelle faggete il cui grado di copertura medio si attesta tra l’80% e il 90%.
Tab. 3 - Valori medi di LAI e grado di copertura per i principali tipi forestali del Trentino (tra parentesi sono riportati i rispettivi errori standard).
| Tipo forestale | LAI | Grado copertura a vista (%) |
Grado copertura densiometro (%) |
|---|---|---|---|
| Faggeta | 3.36 (0.20) | 81.3 (3.85) | 90.9 (1.73) |
| Lariceto | 1.87 (0.31) | 48.3 (7.03) | 83.9 (1.36) |
| Pecceta | 2.60 (0.13) | 63.3 (2.74) | 87.5 (1.24) |
| Pineta | 3.06 (0.27) | 70.8 (4.99) | 89.0 (1.78) |
| Media totale | 2.79 (0.12) | 67.3 (2.36) | 88.2 (0.82) |
Questo fatto è stato confermato anche dal test non-parametrico di Wilcoxon che ha messo in luce delle differenze statisticamente significative nella stima del grado di copertura con l’impiego dei due strumenti (V=9, valore atteso=742.5, varianza=13488.75, p<0.0001). Nello specifico, tali differenze sono sintetizzabili nel fatto che il densiometro sferico tende a restituire valori di copertura significativamente più alti di quelli stimati a vista con una differenza del 20%. Si evidenzia, inoltre, che la deviazione standard interna ai singoli tipi forestali risulta molto più alta nel caso della stima a vista. Questi due tipi d’informazione ci portano a pensare che l’occhio umano è molto sensibile a piccole variazioni nel grado di copertura, causando una potenziale sovrastima dei “vuoti” nella copertura rispetto ai “pieni”. La letteratura suggerisce, invece, che l’impiego del densiometro sferico utilizzando tutti i 96 quadrati tende a sovrastimare il grado di copertura come dimostrato da alcuni autori ([9], [51]).
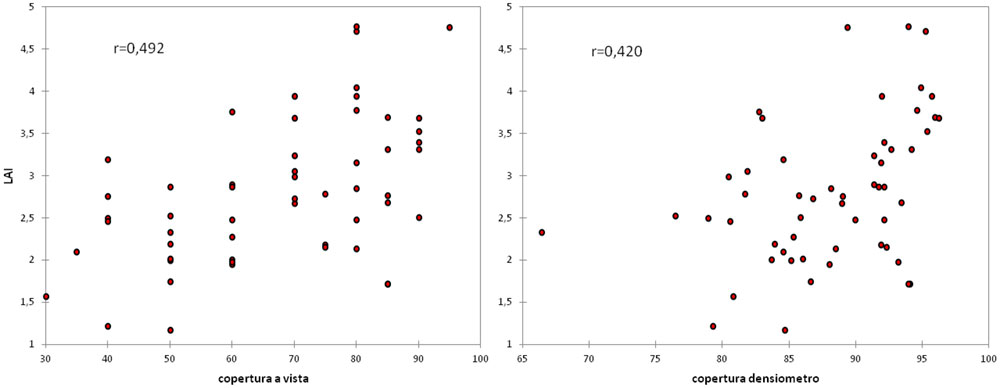
La correlazione tra i valori di LAI e grado di copertura stimato con le due tecniche ha messo in luce una correlazione significativa sia per il confronto tra LAI-grado di copertura a vista (r=0.492, p=0.000) sia per quello LAI-grado di copertura con densiometro sferico (r=0.420, p=0.002). In Fig. 3 sono riportati i due diagrammi di correlazione con il rispettivo coefficiente di correlazione.
Fig. 3 - Diagrammi di correlazione LAI-grado di copertura a vista (a sinistra) e LAI-grado di copertura con densiometro sferico (a destra).
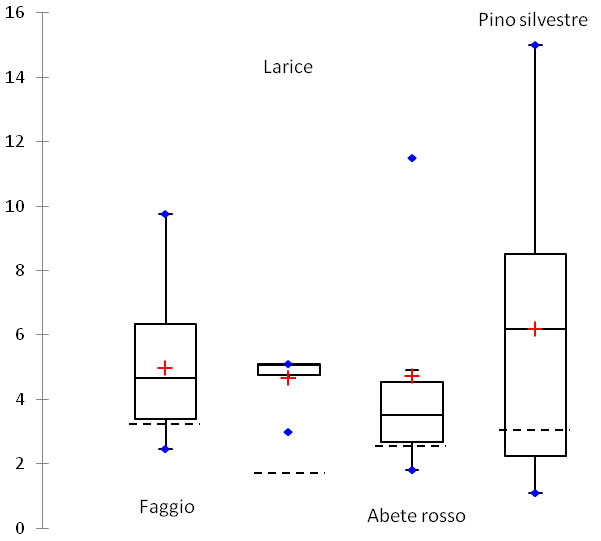
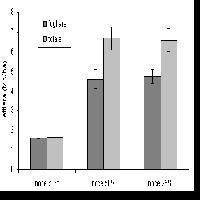
I valori di LAI della presente ricerca variano da un minimo di 1.87 dei lariceti ad un massimo del 3.36 delle faggete. Il confronto tra questi valori e quelli riportati in bibliografia (Appendice 1) evidenzia come i dati di LAI del presente lavoro risultino leggermente più bassi. Complessivamente il LAI medio stimato dalle ricerche analizzate è pari a 4.97 per il faggio, 4.66 per il larice, 4.73 per l’abete rosso e 6.20 per il pino silvestre (Fig. 4). Le principali differenze sono dovute al metodo di stima impiegato, se consideriamo unicamente i lavori di stima del LAI attraverso LAI-2000 e foto emisferiche i valori medi sono in linea con quelli stimati dal presente lavoro: faggio (3.33), larice (2.98), abete rosso (3.49), pino silvestre (2.17).
Fig. 4 - Box plot per i valori di LAI riscontrati in letteratura per tipo forestale (la linea tratteggiata indica i valori medi di LAI nei tipi forestali del Trentino).
Conclusioni
Il presente lavoro ha misurato il LAI e il grado di copertura in un significativo numero di punti di campionamento estratti casualmente all’interno dei quattro principali tipi forestali del Trentino. L’analisi dei dati raccolti ha messo in luce alcuni aspetti di notevole rilevanza che possono essere sintetizzati in una notevole variabilità della distribuzione orizzontale degli alberi e, di conseguenza, delle caratteristiche delle chiome, sia in termini di LAI sia di copertura, nonché una discreta correlazione tra i valori di LAI e quelli del grado di copertura indipendentemente dalla tecnica di stima impiegata.
La differenziazione strutturale mostra che, in Trentino, le formazioni forestali hanno, in genere, una media differenziazione diametrica e una distribuzione regolare delle piante. Tuttavia, non mancano formazioni con distribuzione randomizzata, soprattutto tra le peccete e le pinete.
La notevole differenza tra il grado di copertura stimato a vista e con densiometro sferico ci porta, invece, a dedurre che l’impiego dell’una o dell’altra tecnica negli inventari forestali o nella pianificazione forestale non è indifferente. La stima a vista richiede dei tempi pari a un terzo del tempo di stima con densiometro sferico e anche quest’aspetto deve essere tenuto nella debita considerazione ai fini della scelta della tecnica da adottare. Per quanto concerne la stima a vista del grado di copertura, che rappresenta una pratica usuale nei rilievi speditivi, deve essere condotta da rilevatori esperti e, se possibile, appositamente formati nel contesto territoriale dove andranno ad operare. La presente indagine ha evidenziato come l’attribuzione di un valore puntuale, anziché l’impiego di una classe di copertura, può portare a delle differenze rilevanti rispetto all’impiego di altre tecniche meno influenzate dall’esperienza dell’operatore, come ad esempio i densiometri. Questo fatto può essere dovuto a due ordini di fattori, il primo legato alla scarsa abitudine dei tecnici ad attribuire un valore unico preferendo l’impiego di classi di copertura, il secondo dovuto al rischio di sovrastimare l’elemento meno rappresentato (cielo o copertura fogliare).
La stima del LAI mediante fotografie emisferiche presenta delle interessanti potenzialità d’impiego dovute ai non eccessivi tempi di rilievo in campo, stimabili in circa venti minuti per area di saggio, e nell’analisi delle immagini a video. I valori di LAI stimati nel presente lavoro sono in linea con quelli indicati dalla letteratura internazionale negli stessi tipi forestali e stimati con la medesima tecnica (foto emisferiche o LAI-2000), mentre alcune differenze importanti si notano quando vengono impiegati i metodi diretti.
Ringraziamenti
La ricerca è stata eseguita nell’ambito di un progetto post-doc finanziato dalla Fondazione CARITRO (Cassa di Risparmio di Trento e Rovereto). Gli autori ringraziano CARITRO per il contributo concesso necessario alla realizzazione del presente lavoro.
References
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Online | Google Scholar
Online | Google Scholar
CrossRef | Google Scholar
Online | Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Online | Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
Online | Google Scholar
Online | Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar