Stemwood volume predicting model of Turkey oak high stands in Basilicata (Italy)
Forest@ - Journal of Silviculture and Forest Ecology, Volume 10, Pages 59-67 (2013)
doi: https://doi.org/10.3832/efor1028-010
Published: Sep 02, 2013 - Copyright © 2013 SISEF
Research Articles
Abstract
Stemwood volume predicting model of Turkey oak high stands in Basilicata (Italy). Auxometric studies on the Basilicata forests are few and limited to local contexts. The aim of this study was set up the existing relationships between the volume and tree dimensions for high stands of Turkey oak (Quercus cerris) in Basilicata. The proposed estimate concerns the stemwood volume including branches with diameter > 3 cm. The contribution focuses on the analysis of the most effective forecast models, describing in detail the selected models for assessing the tree volume variation in relation to diameter breast height and total height. The regression coefficients were estimated using a weighted least square regression analysis because variance heterogeneity was constantly observed for the dependent variables. The analysis of residuals among observed and expected values and their distributions show a good fitting of the model to experimental observations. The model proposed may be employed in the forest management as well as in the assessment of stockings of forests ecosystems. The importance of this tool for forest management is confirmed by the remarkable extension of oak forests with Quercus cerris in Basilicata, whose stands are mostly made up by transitional or irregular high stand forests.
Keywords
Tree Volume, Quercus cerris, Volume Equation, Weighted Least Square Regression, Basilicata
Premessa
La determinazione del volume dei soprassuoli forestali rappresenta un momento fondamentale sia per la stima dei boschi da sottoporre a utilizzazione sia per la redazione dei piani di gestione forestale. Nei piani di assestamento forestale si determinano non solamente le masse legnose ma si forniscono indicazioni sulle modalità del futuro trattamento. Si comprende quanto sia importante avvalersi di strumenti estimativi in grado di fornire stime attendibili del volume dei soprassuoli e contemporaneamente di avere una idea precisa sulle incertezze che si hanno nella determinazione delle masse legnose. La carenza di modelli di previsione delle masse arboree e di adeguati studi dendro-auxometrici dei boschi lucani rappresenta da anni un inconveniente nella gestione del patrimonio forestale della regione. Sovente, infatti, si fa ricorso all’utilizzo di tavole di cubatura di validità locale elaborate in altri ambiti territoriali o a tavola di cubatura generali come quelle elaborate per gli Inventari Forestali Nazionali del 1985 ([4]). Le prime lasciano dei dubbi sul piano formale per la carenza di una adeguata analisi statistica, mentre le seconde riuniscono, come per il cerro, in un unico dendrotipo diverse specie e non risultano pienamente rispondenti alle caratteristiche stereometriche dei soprassuoli di ambiti più ristretti, soprattutto di quelli in ambiente mediterraneo. Si consideri, inoltre, che i popolamenti lucani che hanno ormai, dal punto di vista strutturale, la fisionomia della fustaia, possono, per la maggior parte considerarsi dei popolamenti transitori, di origine agamica, che hanno subito negli anni interventi di avviamento all’altofusto e diradamenti che hanno influito sulla forma dei fusti. Si è reso, dunque, necessario elaborare strumenti di stima delle masse legnose che fossero pienamente rispondenti sia all’ambito geografico di interesse sia alla tipologia di soprassuoli indagati, riconducibili a popolamenti transitori o a boschi con struttura irregolare (in evoluzione naturale verso l’altofusto, a struttura generalmente biplana, e con la presenza di piante di grosse dimensioni che rappresentano i rilasci di vecchie utilizzazioni del ceduo).
Il modello previsionale individuato consente di stimare il volume degli alberi, comprensivo di cimale e dei rami fino a tre centimetri di diametro, in funzione del diametro e dell’altezza totale degli alberi. Si tratta di uno strumento particolarmente idoneo a quei casi in cui è richiesta la maggiore precisione possibile nella determinazione dei volumi unitari consentendo così di superare i sovraesposti limiti della letteratura corrente.
Materiali e metodi
L’area di studio è la Regione Basilicata che ha un patrimonio forestale di 355 409 ha ([7]) e i cui soprassuoli a Quercus cerris rappresentano la fisionomia forestale maggiormente diffusa. L’altofusto e i popolamenti transitori di cerro si estendono su una superficie di circa 52 000 ha, dislocati, da Nord a Sud, lungo la catena appenninica.
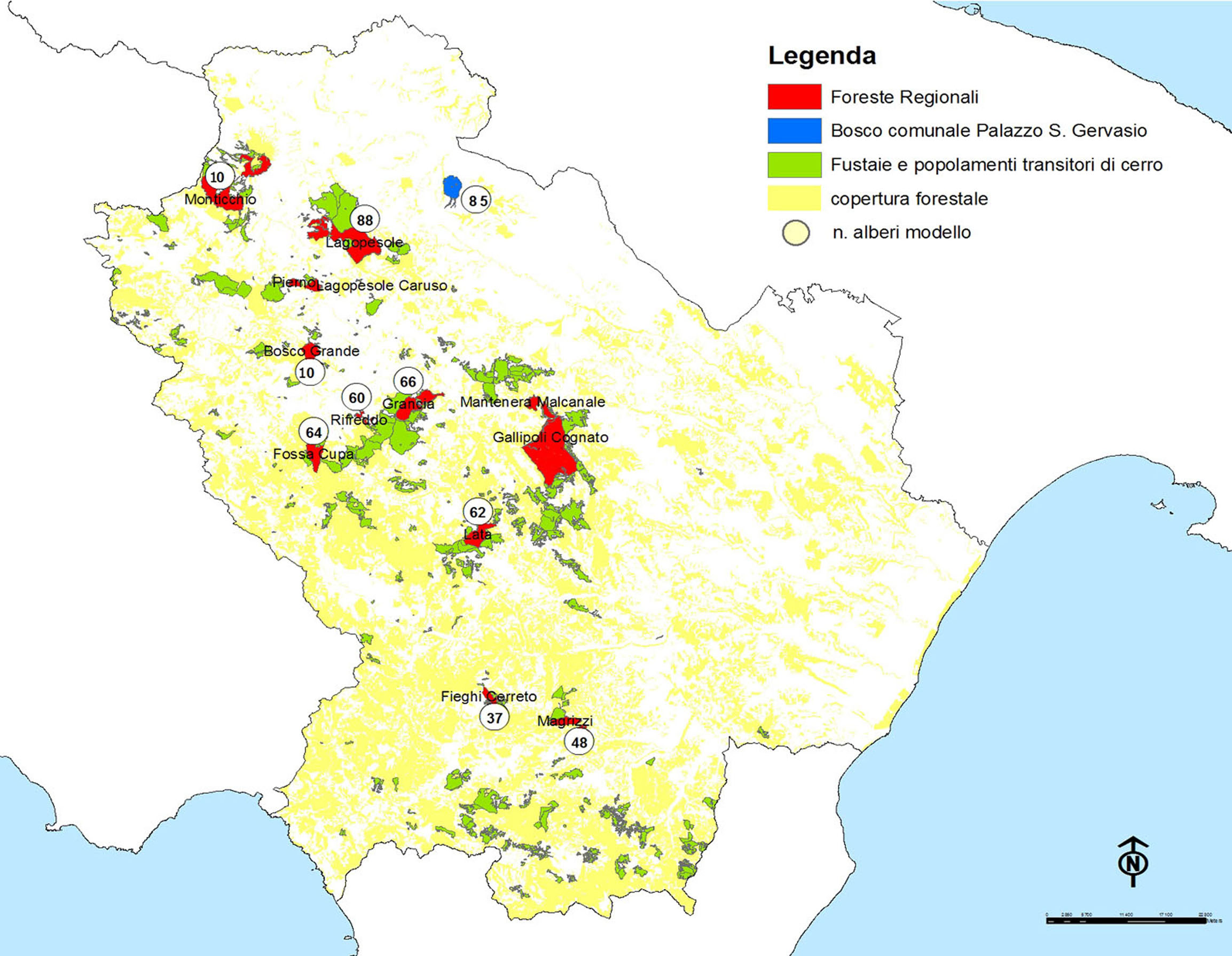
I dati utilizzati per la costruzione della tavola stereometrica a doppia entrata dei boschi ad altofusto di cerro, generalmente popolamenti transitori o a struttura irregolare, sono stati raccolti nel corso di rilevamenti condotti per la realizzazione dei Piani di Assestamento delle Foreste Regionali (Fig. 1). Il patrimonio silvo-pastorale dell’ente Regione Basilicata si estende su una superficie di circa 14 000 ettari, suddivisa in 12 foreste di estensione varia e in cui le cerrete, sempre presenti, rappresentano la fisionomia di gran lunga più rappresentata. A partire dal 2003 la Regione ha intrapreso, grazie anche al cofinanziamento del Ministero dell’Ambiente e Tutela del Territorio, nell’ambito del Programma Operativo Nazionale (PON) di Assistenza Tecnica e Azioni di Sistema (ATAS), Misura 1.2 (Difesa del Suolo), un’azione di pianificazione delle foreste demaniali con la redazione di Piani di Assestamento dei singoli complessi forestali.
Per ognuno dei 595 alberi modello selezionati sono stati rilevati:
- diametro a 1.30 m dal suolo;
- altezza totale degli alberi abbattuti (misurati con rollina metrica);
- circonferenza del fusto ad intervalli di un metro a partire da 0.5 m dal suolo e fino al diametro di svettamento di 3 cm in punta;
- diametri lungo i rami ogni 20 cm fino a 3 cm di diametro.
Il volume dendrometrico di ogni albero modello è stato, quindi, ottenuto sommando il volume dei rami al volume del fusto calcolato con la formula di Heyer.
I dati sono stati sottoposti ad una preventiva analisi allo scopo di verificare (anche in considerazione dell’eterogeneità dei rilievi condotti) l’esistenza di outliers, dati anomali, non consistenti con le altre osservazioni, che potrebbero influire negativamente sulle analisi statistiche.
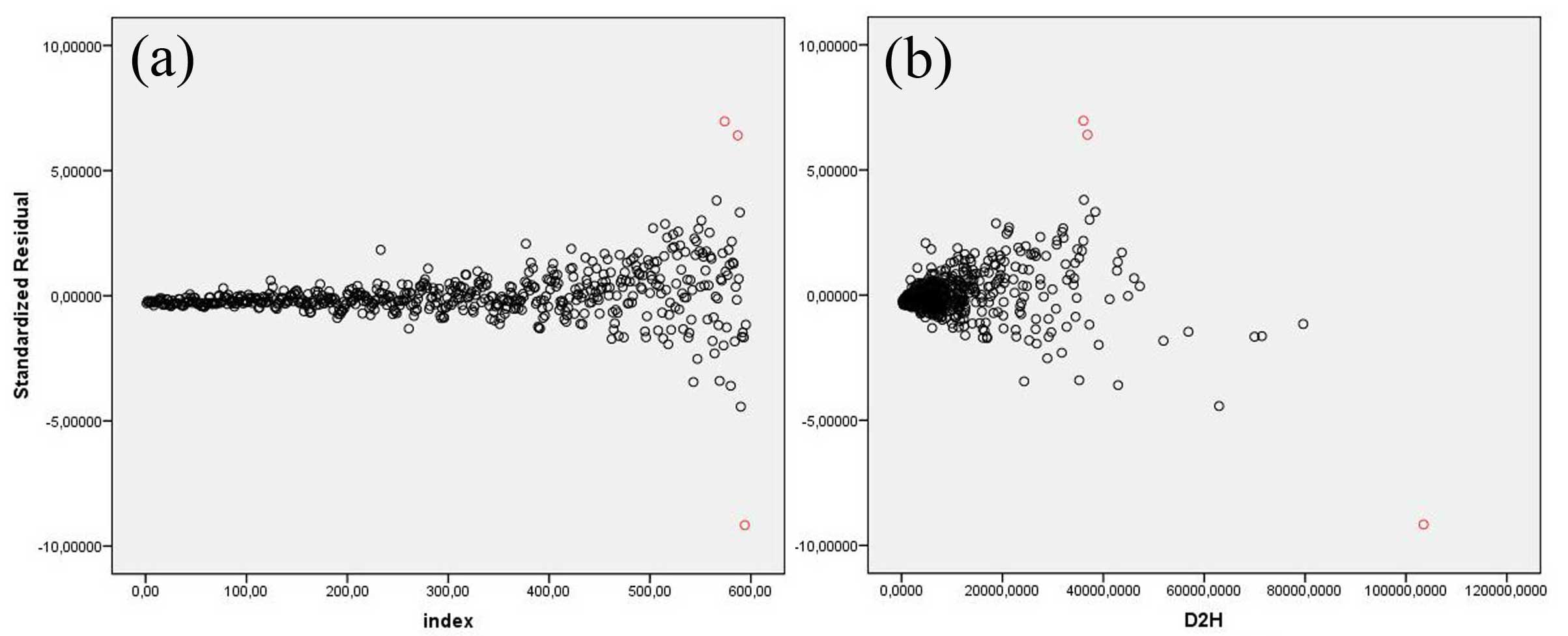
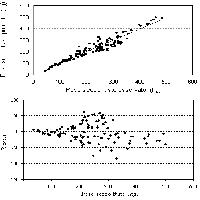
Il plot dei residui standardizzati rispetto agli indici del data set (Fig. 2a) e quello dei residui standardizzati rispetto alla variabile esplicativa D2H (Fig. 2b) evidenzia la presenza di osservazioni che rappresentano probabili outliers.
Fig. 2 - Andamento dei residui standardizzati rispetto agli indici del dataset (a) e della variabile esplicativa D2H.
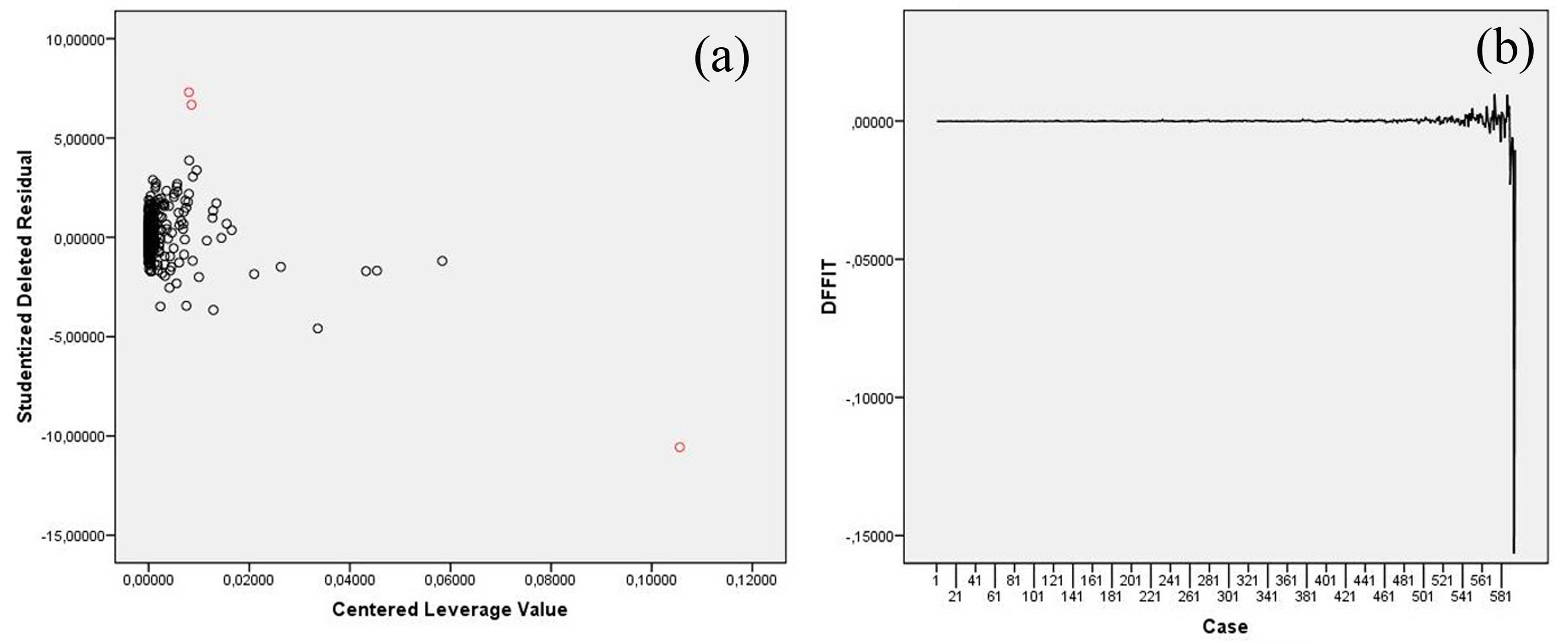
Allo scopo di evidenziare l’influenza (“effetto leva”) degli outliers sulla stima dei parametri di regressione è stata condotta un’analisi grafica dei leverage. Il leverage di un caso è una misura della distanza tra il vettore contenente i valori delle variabili esplicative associate a quel caso e la media dei vettori contenenti i valori delle variabili esplicative associate a tutti i casi. Il grafico (Fig. 3a) che riporta sull’asse delle ascisse il Centered Leverage values e su quello delle ordinate i Residuals Studentized deleted (che più di quelli standardizzati sono in grado di evidenziare i valori anomali in quanto questi ultimi tendono a sottovalutare la grandezza reale dei residui) evidenzia come le osservazioni in esame rappresentino degli outliers, in grado di influire, come suggerito anche dalla statistica DFIT (Fig. 3b), sulla stima dei coefficienti di regressione e sulla loro varianza una volta rimossi dal modello ([22])
Fig. 3 - Residui studentizzati in funzione del Centered Leverage Value (a) e andamento della statistica DFIT (b) per i singoli casi analizzati.
Il dataset finale, dopo la rimozione degli outliers, consta di 592 osservazioni (Tab. 1)
Tab. 1 - Statistica descrittiva delle variabili dimensionali.
| Variabile | n. osserv. | Min | Max | Media | Dev. Std |
|---|---|---|---|---|---|
| D | 592 | 6 | 61 | 21.8 | 9.47 |
| H | 592 | 4.7 | 28.2 | 15.65 | 4.67 |
| Volume | 592 | 0.015 | 3.110 | 0.466 | 0.472 |
Nell’analisi di regressione per l’approntamento di modelli stereometrici un aspetto da valutare preventivamente è il controllo della omogeneità della varianza della variabile dipendente, in quanto, così come ampiamente dimostrato in letteratura ([8], [24], [5], [25], [26], [27], [17]), la condizione di eteroschedasticitàè sempre frequente nelle relazioni che legano le masse arboree alle variabili dimensionali.
Qualora la condizione di omoschedasticità non è rispettata, il vettore degli errori casuali non è caratterizzato da varianza costante: l’analisi condotta con i minimi quadrati ordinari, pertanto, porterebbe a stime non distorte, consistenti, ma poco efficienti ([21], [3], [15]). Gli intervalli di confidenza dei coefficienti stimati, pertanto, risulterebbero poco affidabili in quanto questi ultimi non godono più della proprietà di essere a minima varianza ([25]). La regressione ponderata rappresenta una appropriata procedura di stima ([13]) per ripristinare le condizioni richieste per il vettore dei residui ([28]).
Con il test di Goldfeld-Quandt (Tab. 2), l’ipotesi della omogeneità della varianza viene rifiutata in quanto i valori della variata risultano molto discosti rispetto ai valori critici relativi ai livelli di sicurezza statistica usualmente utilizzati (α = 0.05 e α = 0.01). Si rende necessario, in queste condizioni, adottare dei modelli interpretativi, quali la ponderazione, i cui scarti presentino delle varianze costanti nel campo di escursione delle variabili indipendenti.
Tab. 2 - Stima dei coefficienti della funzione di ponderazione e valore della variabile aleatoria per il test di Goldfeld-Quandt. (d): [cm]; (h): [m]; (Q): variabile aleatoria test Goldfeld-Quandt.
| Var. dipend. | Q | modello di ponderazione σ2 = kZλ (Z = D2H) |
|
|---|---|---|---|
| k | λ | ||
| volume | 70.17 | 0.000367 | 0.779155 |
Per il volume degli alberi, la matrice dei pesi è costruita sulla base della relazione empirica tra la varianza osservata per tali grandezze e le dimensioni degli alberi (diametro ed altezza nel caso di tavole stereometriche a doppia entrata - eqn. 1):
dove Z=d2h nel caso di tavola di cubatura a doppia entrata. I parametri k e λ possono essere desunti dalla letteratura ([9], [18], [30]) o essere stimati con i dati disponibili attraverso analisi di regressione con i minimi quadrati ordinari, come operato in questo studio, o con tecniche di massima verosimiglianza ([6]).
La funzione di ponderazione, ottenuta con l’eqn. 1 e che ha portato alla individuazione dei parametri k e λ, consente di rendere omogenee le varianze della variabile dipendente e permette di avere stime dei coefficienti dei modelli previsionali corrette ed efficienti in quanto a minima varianza.
Per la definizione del modello di regressione ottimale, sulla base di numerosi studi condotti sul fenomeno stereometrico ([24], [25], [26], [17], [19], [29]), si è definito un modello massimo in cui il volume risulta essere funzione delle variabili esplicative D, D2, D3, H, H2 e tutte le possibili combinazioni tra queste variabili.
La procedura adottata nel presente lavoro per la selezione delle variabili esplicative è la stepwise regression ([16], [12], [24]) in cui la scelta delle variabili è stata saggiata tramite un valore elevato di F critico, posto pari a 0.90, in maniera tale da selezionare un numero ridotto di variabili ([6]) e contenere, dunque, il fenomeno della multicollinearità, evitando il ricorso a metodi complessi di riduzione artificiale della collinearità tra le variabili indipendenti ([2], [1], [27], [20]).
Risultati e discussione
Il procedimento utilizzato ha consentito l’ottenimento di un modello operativo ottimale nel quale tutte le variabili selezionate contribuiscono in modo significativo alla spiegazione del fenomeno stereometrico. I risultati sono riassunti nella Tab. 3, dove è riportata la funzione stereometrica definitiva, i relativi parametri stimati, i loro errori standard, l’indice di determinazione (R2) e l’errore standard della stima (ESS). La significatività dei coefficienti di regressione saggiata tramite l’utilizzo del test t di Student. I valori di t dei coefficienti, dati dal rapporto tra il valore stimato del parametro e il suo errore standard, risultano tutti significativamente diversi da zero, con nessuna probabilità (per α= 0.01) che i parametri possano assumere valore nullo.
Tab. 3 - Stima dei parametri del modello di regressione. (D): [cm]; (H): [m]; (V): [m3]; ESS = 0.1330, R2 = 0.946.
| Modello funzionale | Parametro | Beta | Coefficienti | Errore standard dei coefficienti |
t (0.01; 590) |
|---|---|---|---|---|---|
| V = a + bD2H +cD2 | Intercetta | - | 0.00080087 | 0.004217 | 0.1898 |
| D 2 H | 0.6344 | 0.00002825 | 0.000002 | 14.7992 | |
| D 2 | 0.3439 | 0.00031197 | 0.000039 | 8.0222 |
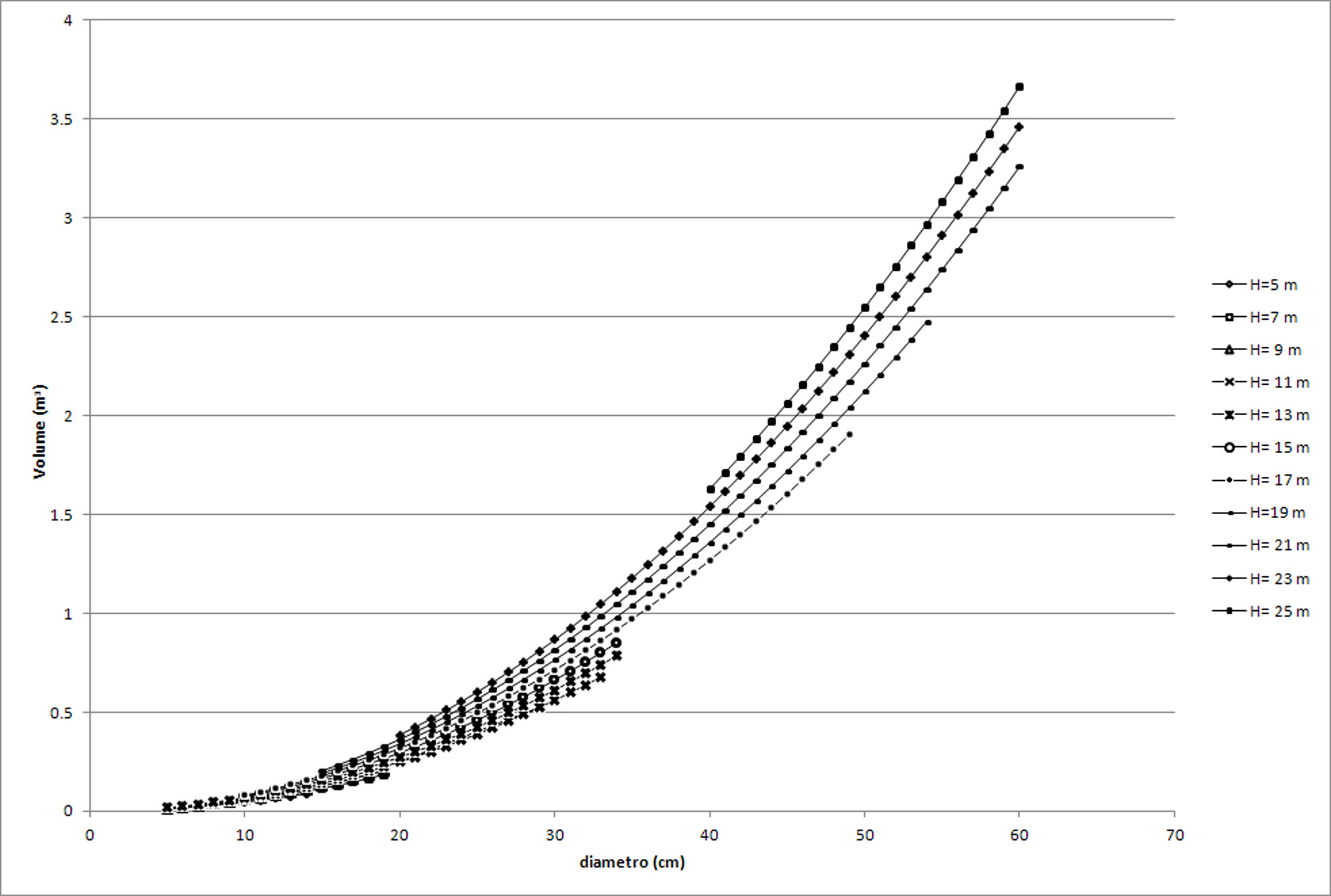
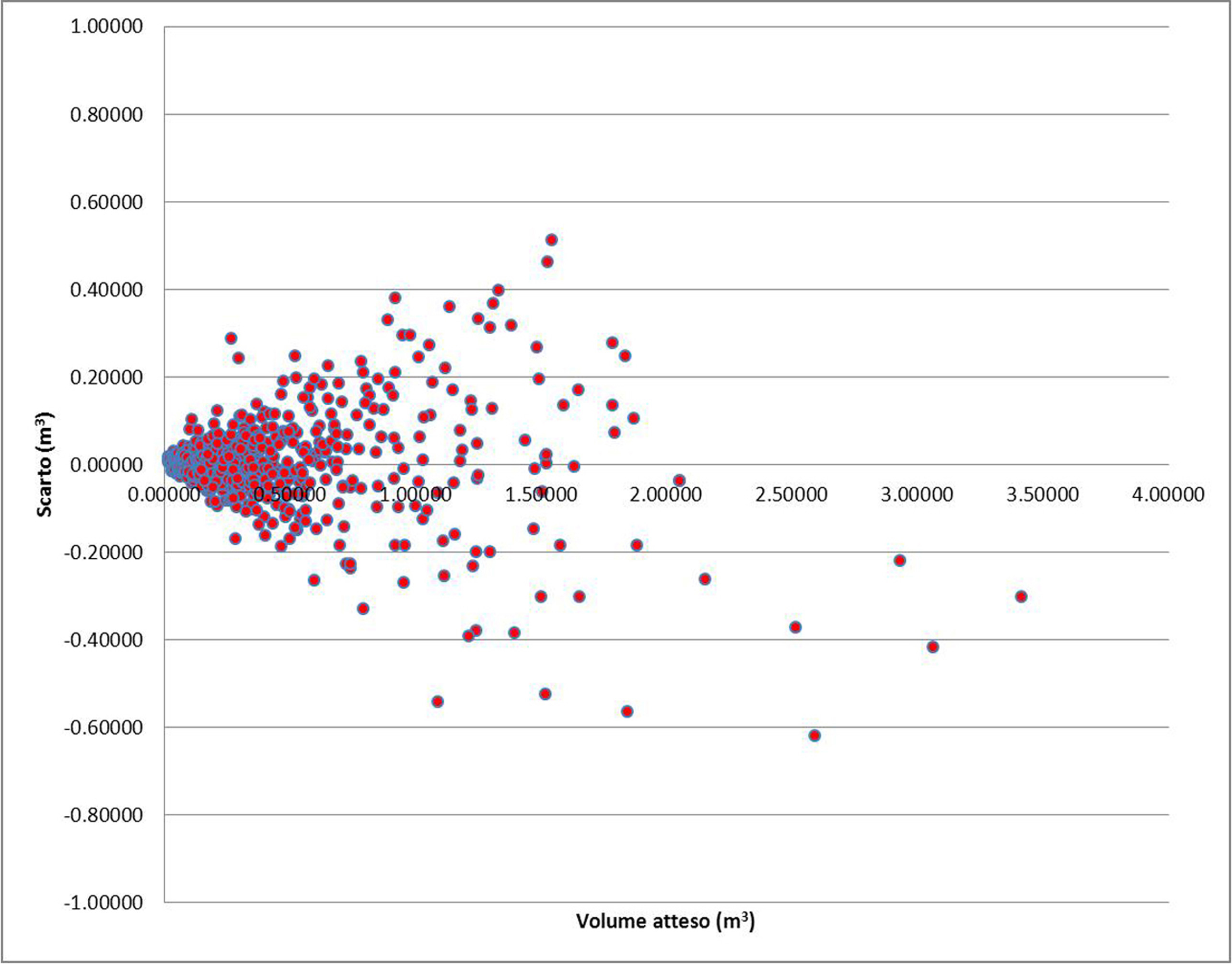
Il controllo della bontà dell’azione di perequazione è stata svolta, preventivamente, attraverso la ricerca di valori ed andamenti non consoni rispetto a quelli attesi; l’analisi (Fig. 4) non ha evidenziato la presenza di valori attesi negativi né tanto meno la presenza di punti di minimo o di flesso nella funzione di perequazione che avrebbero indotto a riformulare il modello.
Una volta verificata l’adeguatezza dell’andamento della equazione di regressione, l’analisi è stata condotta sui residui che forniscono, sotto diversi aspetti, indicazioni valide dell’azione di compensazione ([11], [24]). Alcuni degli indicatori utilizzati (media algebrica dei residui, media quadratica degli scarti assoluti e relativi) si basano sull’entità degli scarti tra valori osservati e valori attesi mentre altri test non parametrici ([23], [24]) si fondano esclusivamente sul segno degli scarti della regressione (variata relativa al test dei segni (U1), variata relativa al test delle successioni (U2), frequenza di scarti di segno opposto nelle diverse classi dimensionali (χ2), con il vantaggio di essere, quindi, indipendenti dal criterio di stima dei parametri e dalla forma del modello di perequazione.
L’analisi dei residui (Tab. 4, Fig. 5) mostra un buon adattamento del modello perequativo alle osservazioni sperimentali: lo scostamento con segno mostra una media algebrica molto prossima allo zero; anche le medie quadratiche degli scarti assoluti e relativi sono contenute ed in linea con i valori attesi per questo tipo di fenomeno. I valori delle variabili aleatorie relative ai test sulla distribuzione dei residui, infine, mostrano anche essi una buona capacità interpretativa, superiore al modello comprendente il solo termine D2H (soprattutto per quanto riguarda i test delle successioni dei segni e del χ2) e al corrispondente modello ottenuto con i minimi quadrati ordinari. Un modello più complesso, contenente, oltre alle predette variabili, il termine D3 e che risultava essere maggiormente performante, come dimostrato dall’analisi dei residui, è stato escluso in quanto presentava un punto di minimo per valori ipsodiametrici contenuti.
Tab. 4 - Valori dei residui e delle variabili aleatorie dei test statistici sulla distribuzione dei residui. Scostamenti di volume: [m3].
| Modello | Media algebrica |
Media quadratica scarti assoluti |
Media quadratica scarti relativi |
Test dei segni (U1) |
Test delle successioni (U2) |
Test χ2 |
|---|---|---|---|---|---|---|
| Volume dendrometrico | 0.000749 | 0.1155 | 0.2245 | -0.04106 | 6.41 | 21.55 |
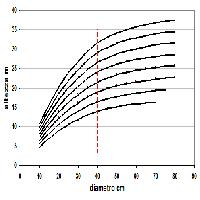
La verifica sugli andamenti del coefficiente di riduzione ordinario non evidenzia tendenze poco consone se non per valori ipsodiametrici molto contenuti: questa lieve difformità rispetto all’andamento ottimale atteso è dovuto, molto probabilmente, alla presenza di termini aggiuntivi al D2H nel modello previsionale adottato. Il modello adottato è teso, però, all’ottimizzazione della funzione stereometrica per il calcolo dei valori volumetrici più che per quelli derivati, quali l’F. L’individuazione del modello perequativo tramite la regressione ponderata consente una corretta analisi dei limiti fiduciari della funzione di predizione, consentendo di individuare (Tab. 5) il range dei possibili valori volumetrici per specifici valori ipsodiametrici.
Tab. 5 - Valori medi attesi del volume dendrometrico (comprensivo dei rami fino a 3 cm) per alcune classi di altezza e di diametro e corrispondenti intervalli fiduciari per α = 0.05. (D): [cm]; (H): [m]; (V): [m3].
| Diametro | Altezza | Volume medio atteso | Limti fiduciari assoluti | Limiti fiduciari % |
|---|---|---|---|---|
| 6 | 6 | 0.011843 | ± 0.011 | ± 58.3 |
| 10 | 6 | 0.048948 | 0.018 | 37.1 |
| 15 | 8 | 0.121845 | 0.032 | 26.4 |
| 20 | 10 | 0.23859 | 0.054 | 22.6 |
| 25 | 12 | 0.407659 | 0.084 | 20.6 |
| 30 | 14 | 0.637527 | 0.124 | 19.5 |
| 35 | 16 | 0.936668 | 0.175 | 18.7 |
| 40 | 18 | 1.313558 | 0.238 | 18.2 |
| 45 | 20 | 1.776671 | 0.315 | 17.7 |
| 50 | 22 | 2.334483 | 0.405 | 17.4 |
| 55 | 24 | 2.995469 | 0.512 | 17.1 |
| 60 | 25 | 3.666404 | 0.621 | 16.9 |
L’analisi si è conclusa con il confronto tra la tavola stereometrica messa a punto per i soprassuoli a Quercus cerris della Basilicata con la tavola stereometrica valida per i soprassuoli di cerro ([28]) messa a punto per l’Inventario Nazionale delle Foreste e dei Serbatoi Forestali di Carbonio (INFC) del 2005.
Si evidenzia, nella tavola INFC, una sistematica sottostima rispetto ai valori volumetrici della presente tavola: le differenze maggiori si denotano per valori ipsodiametrici molto bassi (differenze di circa 30-50%) per ridursi però in maniera progressiva (differenze del 15-20% per valori ipsodiametrici intermedi) fino ad arrivare a differenze tra 2% e il 6% per valori di diametro superiori a 45 cm. Le differenze, ovviamente, sono evidenziabili anche per quanto riguarda il coefficiente di riduzione: le differenze maggiori si registrano per valori ipsodiametrici ridotti e tendono a diminuire via via che aumentano le dimensioni degli alberi e, a parità di altezza, le maggiori differenze si denotano per valori diametrici più ridotti. E’ ipotizzabile che la minore rastremazione dei fusti, nei soprassuoli lucani indagati, sia da ascrivere ai trattamenti di cui essi sono stati oggetto: si tratta in generale, infatti, di popolamenti transitori sottoposti ad interventi di diradamento o di avviamento che hanno ridotto la competizione specifica e di conseguenza la rastremazione dei fusti. La differente pressione competitiva, infatti, condiziona l’occupazione dello spazio da parte degli alberi ([10]) influenzando l’allocazione della biomassa in maniera differenziata nei vari comparti (fusto, rami grossi, rami sottili, ecc.). E’ inoltre da sottolineare che il diametro minimo, sia del cimale che dei rami, preso in considerazione in questo studio è di 3 cm mentre le tavole predisposte per l’INFC utilizzano come soglia il valore di 5 cm e questo contribuisce ulteriormente alla differenza nei valori volumetrici, soprattutto per diametri molto piccoli.
Il confronto ha evidenziato, comunque, che le tavole di validità generale non sono sempre rispondenti, come già riscontrato in letteratura, alle realtà locali e questo risulta essere ancora più valido se ci si riferisce ai soprassuoli boschivi in ambiente mediterraneo ([14]).
Conclusioni
Il lavoro fornisce un importante strumento per la determinazione dei volumi dendrometrici dei soprassuoli di cerro ad altofusto della Basilicata. Si tratta di popolamenti transitori, sottoposti nel passato ad interventi di avviamento e di diradamento. Questa tipologia fisionomico-strutturale è quella maggiormente diffusa in Basilicata: la tavola stereometrica a doppia entrata, dunque, è un valido strumento per chi opera nel settore forestale (amministratori, personale tecnico degli enti, liberi professionisti, ecc.). Le sofisticate tecniche di elaborazione dei dati hanno consentito di ottenere una tavola stereometrica generale della Basilicata, in grado di fornire una stima di elevata precisione nella determinazione dei volumi unitari e una misura esatta delle incertezze che connotano le stime ottenibili con le equazioni approntate ([28]). L’intervallo di predizione delle stime, infatti, risulta attendibile in virtù dell’adozione di una regressione ponderata, necessaria qualora l’omoschedasticità non sia rispettata, come avviene sempre nel caso del volume degli alberi la cui varianza è sempre crescente all’aumentare delle dimensioni degli stessi.
Ringraziamenti
La ricerca è stata realizzata grazie ai dati rilevati durante la fase di redazione dei Piani di Assestamento Forestale delle foreste demaniali della Regione Basilicata. Il progetto è stato cofinanziato dal Ministero dell’Ambiente e Tutela del Territorio, nell’ambito del Programma Operativo Nazionale (PON) di Assistenza Tecnica e Azioni di Sistema (ATAS) Misura 1.2 (Difesa del Suolo), Linea di Attività 2.2 “Supporto per problematiche di notevole complessità”. Si ringraziano i rilevatori coinvolti nella redazione dei Piani di Assestamento e l’INEA Basilicata che ne ha coordinato la realizzazione.
References
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
CrossRef | Google Scholar