TaCAL: a "tariffs" system of tree volume and phytomasses of forest tree species in Calabria (southern Italy)
Forest@ - Journal of Silviculture and Forest Ecology, Volume 14, Pages 60-74 (2017)
doi: https://doi.org/10.3832/efor2278-013
Published: Feb 27, 2017 - Copyright © 2017 SISEF
Research Articles
Guest Editors: ALForLab Project (PON03PE_00024_1 - PON R&C- PAC 2007-2013)
« Public-private lab for the application of innovative technologies with high environmental sustainability in the forest-wood-energy chain »
Collection/Special Issue: Alessandro Paletto (CREA, Trento), Giorgio Matteucci & Mauro Maesano (CNR-ISAFOM)
Abstract
In the frame of the ALFORLAB project, a harmonised set of tree volume (and biomass) single entry tables (“tariffs”) was developed for the main 20 forest species of Calabria (Southern Italy), to outline the “coordinates” of volume expression for inventory purposes at both regional and forest planning level. The system, called TaCAL, was based on the double entry volume and biomass functions of the Italian National forest Inventory - INFC 2005 -, and was built studying the height/dbh relationships on 2300 trees measured during the INFC campaign in Calabria, on over 300 sampling plots randomly distributed. For each of the 20 species, or group of similar species, the tariff system is articulated into 9 h/d relationship curves, which are in turn related to corresponding single entry tables of tree volume (stem and branches with dbh above 5 cm), and respective biomass tables. According to INFC 2005 stereometric equations, TaCAL system is suitable for both high forests and coppices. TaCAL provides a uniform volume and biomass estimation system for all main forest species of Calabria as well as, under certain conditions, a unique criterion of expression of the site fertility. TaCAL tariff system has already been integrated into the construction of forecasting models of timber volume and biomass based on angle count samplings, at forest management scale. TaCAL has also provided the basis for ground truth volume estimates to develop forecast models through remote sensing LiDAR data. It must be emphasized that TaCAL represents the first case in Italy in which single tree data by INFC field surveys were used to carry out a comprehensive dendrometric system at a regional level.
Keywords
Volume Tables, Tariff Systems, Biomass Tables, Forest Planning, Calabria
Introduzione
Come è noto, per “tariffe” si intendono serie di tavole di cubatura a una entrata (derivate da sottostanti funzioni stereometriche a doppia entrata), differenziate in base a diversi andamenti standardizzati della relazione altezza/diametro (h/d) dei soggetti arborei. Normalmente vengono realizzati “sistemi di tariffe” costituiti da varie serie omogenee, differenziate “per valenza dendrologica” rispetto alla specie o gruppi di specie alle quali sono applicabili ([6]).
Fin dagli anni ’ÂÂ50, sistemi di questo tipo sono stati alla base degli inventari con finalità assestamentali nella Regione Trentino-Alto Adige ([2], [10]) e più recentemente per la Regione Friuli Venezia-Giulia ([4]). Sistemi tariffari sono stati realizzati anche per le principali specie forestali dell’Emilia-Romagna ([9]), per alcune specie di conifere in Sicilia ([1]), per il Pino silvestre e il Larice nelle Regioni Valle d’Aosta e Piemonte ([7], [8]).
Come già menzionato, solitamente i sistemi di tariffe si basano su una sottostante funzione stereometrica a doppia entrata [v = f (d, h)] di specie o gruppo di specie, adottata come riferimento stereometrico, mentre gli andamenti standard della relazione h/d vengono appositamente studiati in sede di sviluppo del sistema tariffario con apposite campagne di rilievi ipsometrici nell’ambito territoriale di validità. Caso classico è quello delle “Tariffe della Regione Trentino - Alto Adige” ove le sottostanti tavole di cubatura a doppia entrata sono quelle della nota raccolta di Grundner-Schwappach ([5]), valide per le principali specie forestali centro-europee e semplicemente “adottate” in Trentino, pur se a seguito di successivi parziali controlli di coerenza dendrometrica ([11]) e recentemente modellizzate e ristilizzate ([10]).
La definizione delle serie di relazioni h/d, le quali, a parità di diametro, esprimono “quote” più o meno elevate del rapporto citato da ascrivere prevalentemente a diverse condizioni di fertilità (purché anche a parità di classe cronologica, nei popolamenti coetaneiformi), avviene solitamente a partire da una “curva guida” che perequa tale relazione in condizioni “medie”. Detta curva viene poi (di solito) isomorficamente riprodotta verso l’alto e verso il basso a “distanze” ipsometriche costanti. Tali distanze vengono più o meno convenzionalmente scelte (sono in genere di 2-3 m al diametro medio di 35 cm), fino creare 3-4 curve di evoluzione della relazione h/d superiori e rispettivamente inferiori a quella media e addivenire quindi al fascio di 7-9 curve guida definitive della serie per una determinata specie. Tale fascio di curve deve essere in grado di rappresentare il campo di variazione delle situazioni ipsometriche evidenziato dai popolamenti della specie considerata nel territorio di validità del sistema.
In riferimento allo studio delle “curve guida” h/d, i termini correnti di “curva ipsometrica” non dovrebbero essere adottati in quanto teoricamente riferibili solo a relazioni che esprimono la variazione media probabile dell’altezza sul diametro di soggetti appartenenti a popolamenti coetanei (o della stessa classe di età). In tali casi la relazione esprime il contributo “puro” del diametro alla variazione dell’altezza, non interferito dall’età.
Nella prassi della realizzazione di sistemi di tariffe di cubatura si adottano invece i termini di curva ipsometrica anche nei casi di relazione media probabile h/d per soggetti non necessariamente coetanei (e spesso appartenenti anche a strutture differenziate, dal monoplano al multiplano). La differenza non è solo terminologica e in realtà sottende implicazioni dendrometriche di una certa rilevanza, nel caso di popolamenti non coetanei, laddove la “curva ipsometrica” viene quasi sempre costruita considerando nel campione soggetti di un ampio intervallo di età. La variazione diametrica non è quindi in tal caso pura risultanza della potenzialità intrinseca o microstazionale dei soggetti (della stessa età) di raggiungere una determinata altezza a un certo diametro, ma anche dell’età che, in sé stessa, influenza fortemente il diametro. Siamo quindi di fronte ad una sorta di “pseudo-curva di sviluppo” dell’altezza sul diametro che sottende anche l’influenza dell’età. Le classiche curve di sviluppo (parametro su età) hanno come è noto forma logistica, con una prima parte a concavità verso l’alto e una seconda, più ampia, a concavità verso le ascisse, per il tramite di un punto di flesso. È legittimo ritenere che anche la relazione h/d in popolamenti (variamente) non coetanei (stragrande maggioranza dei casi di derivazione del campione nella costruzione di tariffe), essendo anche condizionata dall’età dei soggetti, sia di tipo pseudo-logistico, con un punto di flesso molto precoce (per diametri molto piccoli). Tuttavia tale punto di flesso si verifica solitamente al di sotto dei diametri minimi correnti di validità delle tavole (7.5-5.0 cm). Si vedrà in seguito come tali considerazioni abbiano influito sulla scelta della struttura del modello perequativo ipsometrico standard in questo studio.
È opportuno sottolineare che, come si può desumere da quanto detto finora, nella costruzione di tali sistemi stereometrici non dominano esigenze di fitting ai fini previsionali di andamenti ipsometrici (con tutte le conseguenze sul piano delle inferenze statistiche e delle analisi di performance della regressione), quanto invece approcci, in parte pragmatici, tendenti ad oggettivizzare il più possibile il loro “andamento medio probabile” con un approccio analitico che pervenga alla definizione di una funzione perequatrice.
I dati per la realizzazione del sistema ipsometrico guida di TaCAL
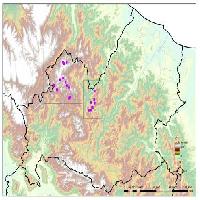
I rilievi ipsometrici dell’INFC 2005 (2330 coppie di dati “nativi” h e d, 729 per le conifere e 1601 per le latifoglie), raccolti negli oltre 300 punti inventariali di Terza fase INFC realizzati in Regione Calabria (Fig. 1), hanno costituito la base per lo studio dell’impianto ipsometrico TaCAL (curve tariffarie guida della relazione h/d delle varie specie). I dati salienti di numerosità del campione per specie o gruppo di specie e i dati significativi dei relativi intervalli di diametro e di altezza sono riportati nelle Tab. 1 e Tab. 2. Si tratta del primo caso nel quale i dati nativi INFC sono stati impiegati per la costruzione di modellistica ipsometrica regionale.
Fig. 1 - Collocazione dei punti di campionamento INFC 2005 di terza fase nella Regione Calabria. Le zone in giallo sono le quattro aree studio del progetto AlForLab.
Tab. 1 - Dati salienti di numerosità del campione per il gruppo di specie delle Conifere e dati significativi dei relativi intervalli di diametro e di altezza.
| Specie o gruppo di specie | Numero di alberi modello |
Diametro a 1.3 (cm) | Altezza (m) | ||||
|---|---|---|---|---|---|---|---|
| medio | massimo | minimo | media | massima | minima | ||
| Abete bianco | 92 | 29 | 130 | 5 | 16.5 | 39.3 | 3.4 |
| Douglasia | 87 | 33 | 54 | 9 | 22.3 | 31.4 | 6.9 |
| Pino laricio/nero/loricato | 423 | 33 | 106 | 5 | 18.5 | 39.0 | 3.4 |
| Pino d’Aleppo | 51 | 21 | 53 | 5 | 8.8 | 13.2 | 4.0 |
| Pino marittimo | 20 | 38 | 58 | 19 | 16.8 | 26.6 | 10.6 |
| Pino domestico | 23 | 34 | 76 | 5 | 12.8 | 23.4 | 3.8 |
| Pini alloctoni | 18 | 27 | 41 | 14 | 14.6 | 25.6 | 9.1 |
| Cipressi | 15 | 24 | 40 | 10 | 10.2 | 13.5 | 6.9 |
| Totale | 729 | - | - | - | - | - | - |
Tab. 2 - Dati salienti di numerosità del campione per il gruppo di specie delle Latifoglie e dati significativi dei relativi intervalli di diametro e di altezza.
| Specie o gruppo di specie | Numero di alberi modello |
Diametro a 1.3 (cm) | Altezza (m) | ||||
|---|---|---|---|---|---|---|---|
| medio | massimo | minimo | media | massima | minima | ||
| Faggio | 432 | 27 | 115 | 5 | 17.8 | 38.0 | 4.5 |
| Castagno (non da frutto) | 268 | 17 | 111 | 5 | 13.3 | 27.4 | 5.0 |
| Cerro | 179 | 24 | 63 | 5 | 14.0 | 32.8 | 4.7 |
| altre Querce caducifoglie | 69 | 24 | 94 | 6 | 12.3 | 29.8 | 5.0 |
| Roverella | 90 | 24 | 81 | 5 | 10.6 | 21.0 | 2.3 |
| Leccio | 130 | 16 | 64 | 5 | 9.2 | 21.9 | 3.1 |
| Sughera | 26 | 28 | 45 | 9 | 8.9 | 18.0 | 4.6 |
| Aceri | 31 | 20 | 50 | 5 | 12.9 | 27.4 | 6.1 |
| Frassini (prev. Orniello) | 26 | 11 | 18 | 5 | 8.9 | 14.5 | 5.7 |
| Carpini | 31 | 17 | 50 | 7 | 10.9 | 20.1 | 6.3 |
| Ontani | 141 | 25 | 52 | 5 | 16.3 | 31.0 | 3.0 |
| Eucalitti | 95 | 16 | 43 | 5 | 11.3 | 23.8 | 3.3 |
| Robinia | 27 | 14 | 43 | 5 | 8.0 | 16.7 | 1.6 |
| altre latifoglie maggiori | 11 | 28 | 84 | 8 | 11.3 | 29.7 | 5.6 |
| altre latifoglie minori | 45 | 14 | 30 | 5 | 6.3 | 19.3 | 1.9 |
| Totale | 1601 | - | - | - | - | - | - |
Circa gli alberi modello di cui sopra va sottolineato che essi appartengono solo ai sottoinsiemi di 10 soggetti che sono stati misurati in ogni area di saggio INFC della Calabria, oltre che per il diametro, anche per l’altezza. Si tratta quindi dei soli soggetti dotati di altezza nativa “vera”, cioè desunta da reali misure in campo. Va infatti ricordato che il processo di elaborazione dei dati ipsometrici INFC ([13]) prevedeva che a tutti i soggetti rilevati nell’area di saggio fosse comunque associata una altezza stimata modellisticamente a posteriori, tenendo conto (i) dell’andamento generale ipsometrico medio (nazionale) della specie e (ii) di un adeguamento locale attuato con la considerazione della variabile altezza dominante dell’area di saggio (altezza media dei 3 soggetti più grossi, indipendentemente dalla specie). Tali dati, che in tempi successivi a questo studio sono stati resi disponibili dal Corpo Forestale dello Stato per tutte le aree di saggio INFC di Terza fase, sono quindi ben superiori in numero (anche per la Calabria) al campione adottato in questo studio (con ben più ampia rappresentatività di tutte le specie), ma sono stati ritenuti inadatti in questo contesto in quanto esito di processi di stima modellistica che, per quanto adeguati nel contesto delle elaborazione dei dati INFC, non costituiscono reali dati misurati.
In funzione di tale circostanza, va sottolineato che la rappresentanza nel campione ipsometrico delle varie specie forestali principali (20 tra conifere e latifoglie, di tutti i piani altitudinali) si può ritenere sostanzialmente proporzionale alla loro diffusione in termini di superficie nella realtà della Calabria, con le specie più diffuse largamente più rappresentate. Indubbiamente alcune specie minoritarie sono quindi scarsamente rappresentate nel campione INFC adottato. È da notare tuttavia che la presenza di un disegno di campionamento rigoroso quale è quello dell’INFC e il rilievo di soggetti in piedi casualmente individuati nei punti di campionamento inventariali depone per un’ottima rappresentazione territoriale del fenomeno.
Metodologia
I modelli stereometrici a doppia entrata sottostanti al sistema TaCAL
Per quanto attiene alle funzioni stereometriche a doppia entrata sottostanti al sistema TaCAL, si è ritenuto obbligatorio adottare quelle più recenti dell’Inventario nazionale delle Foreste e dei Serbatoi forestali di Carbonio ([12]). Nell’organizzare un sistema moderno di interpretazione dendrometrica delle formazioni forestali della Calabria era infatti da salvaguardare innanzitutto la perfetta compatibilità della modellistica con i riferimenti stereometrici nazionali più recenti e autorevoli. Inoltre l’impianto modellistico INFC (e quindi anche del sistema TaCAL), risulta esteso non solo alla previsione dei volumi dei soggetti arborei ma anche a quella delle rispettive fitomasse anidre (fondamentali nelle stime riferite al sequestro forestale di carbonio) siano esse riferite alla sola componente legnosa fino a 5 cm di diametro che alla biomassa totale (comprensiva di fascina, fogliame e ceppaie fuori terra). Ciò ha permesso di costruire il primo sistema tariffario regionale italiano esteso al peso secco (più precisamente, anidro) delle fitomasse. Si noti che i modelli INFC derivano dalla raccolta di alberi modello nell’ambito di una vasta campagna nazionale dedicata, rivolta a soggetti appositamente scelti, abbattuti e misurati (con intensa attività anche di laboratorio) e non sono invece derivanti, come spesso accade, da utilizzazioni ordinarie che spesso rappresentano in modo anomalo la “facies media statistica” degli alberi delle varie specie presenti sul territorio nazionale o regionale.
Il modello ipsometrico del sistema TaCAL
Nella costruzione delle curve guida primarie di gruppo di specie del sistema ipsometrico TaCAL si è adottato un approccio concettuale come quello descritto nel paragrafo introduttivo e si è impiegata una struttura classica del modello perequativo ipsometrico [h = f (d)] proposta da Curtis ([3]) del tipo (eqn. 1):
dove h è l’altezza totale del soggetto arboreo, d è il diametro ad 1.3 m e b4, b5, b6 sono i coefficienti del modello perequativo, variabili con il gruppo di specie.
La denominazione e numerazione dei coefficienti rientra in una nomenclatura generale del sistema TaCAL per la quale i coefficienti dei modelli ad una entrata di volume (vedi oltre) hanno il simbolo b seguito da un indice da 1 a 3, nuovamente il simbolo b, seguito da un indice da 4 a 6 per quelli ipsometrici delle serie ipsometriche medie h/d di conifere e latifoglie e il simbolo c, con indice variabile da 1 a 9 quale identificativo della serie ipsometrica tariffaria di ogni gruppo di specie, corrispondente a un moltiplicatore da 1.6 a 0.4 (con passo 0.15, in diminuzione) dell’altezza della serie-guida media h/d per l’ottenimento dell’altezza specifica riferita alla serie ipsometrica di volta in volta prescelta (da 1 a 9).
Il modello ha caratteristiche importanti, quali la presenza di un punto di flesso a diametri che normalmente si rivelano molto precoci (circostanza congruente con quanto affermato in precedenza) ed essendo asintotico, mostra una adeguata stabilità del gradiente di aumento dell’altezza per i diametri elevati (con pendenza moderata), aspetto che favorisce una buona capacità di estrapolazione, appunto per i diametri elevati, estranea ad altri approcci modellistici.
La “forma” e le “quote” del sistema ipsometrico guida TaCAL
In una prima fase di approfondita analisi della “forma” dei fenomeni ipsometrici delle varie specie facenti parte del campione si è notato come fosse pragmaticamente attuabile una scelta semplificativa di messa a punto di soli due sistemi ipsometrici per i grandi gruppi delle conifere e delle latifoglie. È apparso infatti plausibile costruire un’unica curva guida “media” della relazione h/d per ciascuno dei due grandi gruppi di specie, risultante di una delle due specifiche configurazioni numeriche dei coefficienti del modello. Come si è detto sopra, dalla curva “media” sono stati generati poi 4 andamenti ipsometrici superiori e 4 inferiori (equidistanti) per un totale di 9 livelli standard di “quota” della relazione h/d contrassegnati dagli indicatori di tariffa da 1 (tariffa “migliore”) a 9 (tariffa “peggiore”), essendo 5 l’indicatore della curva h/d “media”.
È forse opportuno fare qualche osservazione circa le conseguenze di tale scelta metodologica. In primo luogo occorre ammettere che non si tratta di una scelta ordinariamente adottata nella costruzione dei sistemi guida ipsometrici tariffari in Italia. Tuttavia, essa implica notevoli semplificazioni che sono state giudicate prevalere su qualche controindicazione.
In relazione alla semplificazione introdotta in termini di effetti sul piano computazionale e di implementazione informatica dei modelli, si pensi che essa è stata in parte obbligata. Infatti, come si vedrà meglio più avanti, il sistema TaCAL, essendo esteso alla stima di due tipi di fitomasse oltre che del volume, non permette il raggruppamento di specie stereometricamente affini, consuetudine di altri sistemi tariffari, a causa di profonde diversità nei pesi specifici dei legnami di specie pur raggruppabili sul piano degli andamenti stereometrici (volume in funzione di d e h). La conseguenza del raggruppamento “pragmatico” in soli due sistemi degli andamenti ipsometrici standard ha determinato la presenza nel sistema di sole 18 (2×9) equazioni ipsometriche standard invece che di 180. La circostanza può non essere di capitale importanza in un quadro di elaborazione centralizzata e standardizzata dei rilievi assestamentali, ma assume diversa connotazione quando le elaborazioni avvengono a livello di singoli professionisti, magari negli ambiti semplificati e personali di semplici fogli di calcolo.
Sul piano concettuale, la scelta in discussione consente poi agli operatori di costruirsi più facilmente un quadro mentale comparato di riferimento dei fenomeni ipsometrici delle specie calabresi.
Occorre notare che la scelta in discussione ha comunque conseguenze esclusivamente sulla più o meno accentuata adattabilità al sistema di ogni specifico caso e specie esclusivamente in termini di “forma” della relazione ipsometrica semplificata a sole due facies, la cui influenza sulla formazione dei volumi individuali dei soggetti arborei (obiettivo estimativo finale del sistema tariffario TaCAL) è largamente minoritaria, anche perché correlata prevalentemente alla zona dei diametri minori (con minore incidenza sulle provvigioni ad ettaro). Ben altra è invece l’influenza della “quota” della relazione h/d e tale aspetto è garantito anche nel sistema semplificato adottato, che è pur sempre articolato su ben 9 livelli. Si consideri peraltro che nel confronto tra l’influenza dovuta ad un certo aumento percentuale del diametro (a parità di altezza) e quello di un analogo aumento percentuale di altezza (a parità di diametro) il primo ha influenza circa doppia sul volume finale di un soggetto arboreo.
Risultati
Gli andamenti ipsometrici medi di conifere e latifoglie
Lo studio del modello perequativo [1] adottato per l’insieme degli alberi modello dell’altezza delle Conifere e delle Latifoglie, ha portato alle configurazioni di coefficienti della Tab. 3.
Tab. 3 - Coefficienti del modello della funzione guida "media" della relazione h/d per ciascuno dei due grandi gruppi di specie.
| Gruppo di specie | b 4 | b 5 | b 6 |
|---|---|---|---|
| conifere | 1.663867 | 0.995766 | 0.025065 |
| latifoglie | 0.338638 | 0.850896 | 0.033509 |
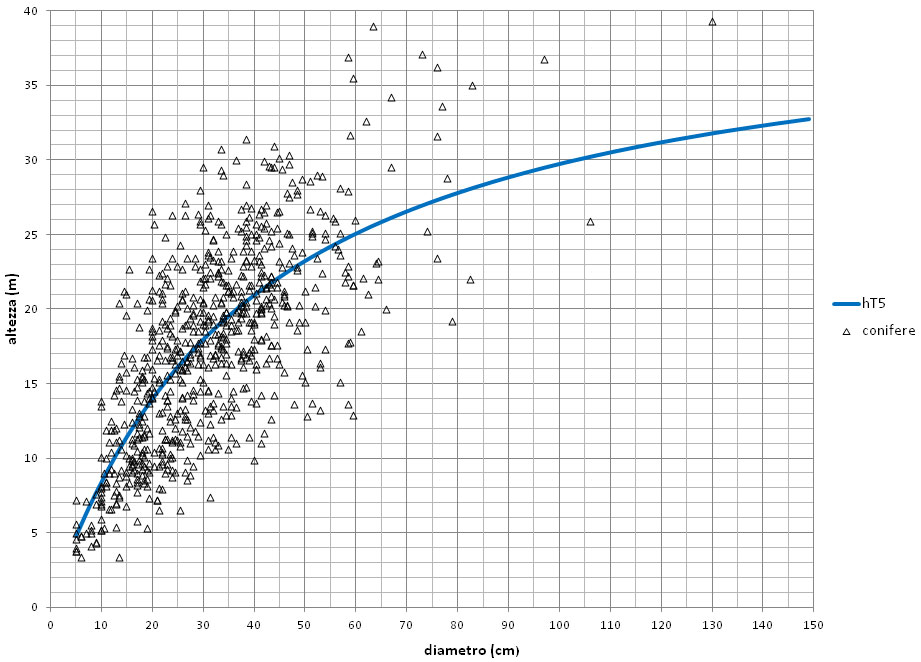
Le Fig. 2 e Fig. 3 mostrano l’andamento delle funzioni rispetto ai dati ipsometrici utilizzati per costruirle. Nella Fig. 4, viene mostrato il confronto fra i due andamenti.
Fig. 2 - Dati ipsometrici e andamento perequativo della curva guida “media” (hT5) della relazione h/d per le conifere.
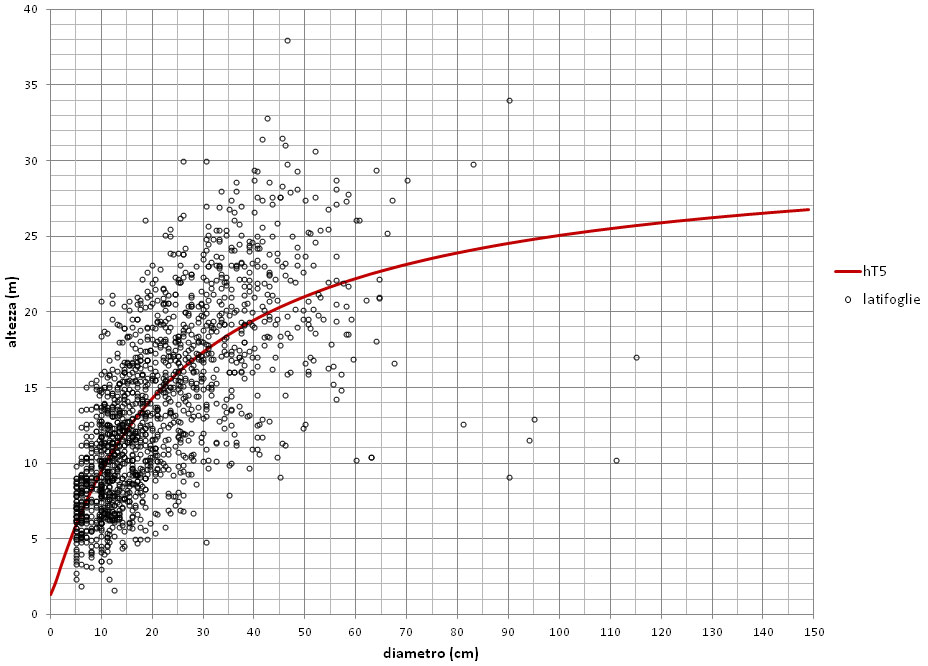
Fig. 3 - Dati ipsometrici e andamento perequativo della curva guida “media” (hT5) della relazione h/d per le latifoglie.
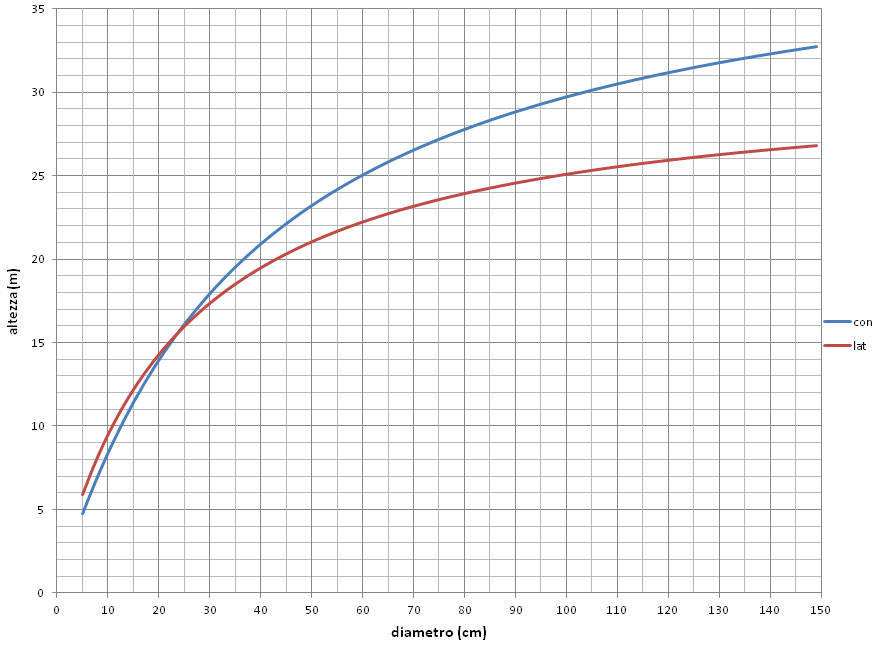
Fig. 4 - Andamenti raffrontati delle due curve guida “medie” della relazione h/d (hT5) per ciascuno dei due grandi gruppi di specie.
In quest’ultima figura si può riscontrare come le specie di conifere nel loro complesso mostrino in modo abbastanza generalizzato, fino al diametro di 25 cm, (i) una pendenza della funzione interpretativa leggermente minore, con altezze medie leggermente più basse (-10%, rispetto alle specie di latifoglie) per poi (ii) invertire la tendenza ed evolvere, a parità di diametro, su quote ipsometriche medie decisamente più elevate delle latifoglie, quote che già a circa 45 cm di diametro cominciano a superare del 10% le altezze nella comparazione con le latifoglie, per poi aumentare progressivamente il divario relativo. Specie emblematiche di tale comportamento sono da una parte l’Abete bianco e il Pino laricio e dall’altra il Castagno e il Faggio, cioè le principali del panorama forestale montano calabro.
È da notare che le funzioni evidenziano gli attesi punti di flesso intorno a 2-3 cm, peraltro al di fuori del campo di validità del sistema.
Le Tab. 4 e Tab. 5 evidenziano le consuete statistiche ordinary least square (OLS) sui coefficienti dei modelli. Si nota come l’apporto esplicativo del coefficiente b4 (intercetta del modello quadratico al denominatore del secondo termine) non sia significativo, in entrambi i casi. Tuttavia si è deciso di mantenere la configurazione del modello nella versione originale di Curtis per future necessità che eventualmente emergessero di “personalizzare” i modelli ipsometrici guida per le specie principali (Faggio, Castagno, Cerro, Pino laricio e Abete bianco). Si è notato infatti nelle analisi particolari di modellizzazione con i soli alberi modello di determinate specie che, mentre il coefficiente del regressore d2 è sempre significativo, gli altri due lo sono in modo vario rispetto alle specie considerate nei loro specifici fenomeni di esplicazione ipsometrica. Sotto il profilo dell’eventuale implementazione di sistemi informatici di elaborazione di dati assestamentali è sempre utile prevedere modelli invarianti nella struttura e quindi nel numero dei coefficienti, scelta che in questa caso non porta a particolari perturbazioni nelle stime.
Tab. 4 - Stimatori e relative statistiche OLS dei modelli della funzione guida “media” della relazione h/d per il gruppo delle conifere.
| Conifere | Stima | ES | t-value | p-level | Lo. Conf | Up. Conf |
|---|---|---|---|---|---|---|
| b4 | 1.663867 | 2.012043 | 0.82695 | 0.408535 | -2.28625 | 5.613983 |
| b5 | 0.995766 | 0.146766 | 6.78471 | 0.000000 | 0.70763 | 1.283902 |
| b6 | 0.025065 | 0.002426 | 10.33020 | 0.000000 | 0.02030 | 0.029829 |
Tab. 5 - Stimatori e relative statistiche OLS dei modelli della funzione guida “media” della relazione h/d per il gruppo delle latifoglie.
| Latifoglie | Stima | ES | t-value | p-level | Lo. Conf | Up. Conf |
|---|---|---|---|---|---|---|
| b4 | 0.338638 | 0.650825 | 0.52032 | 0.602911 | -0.937908 | 1.615184 |
| b5 | 0.850895 | 0.074658 | 11.39719 | 0.000000 | 0.704459 | 0.997332 |
| b6 | 0.033509 | 0.001717 | 19.51779 | 0.000000 | 0.030141 | 0.036876 |
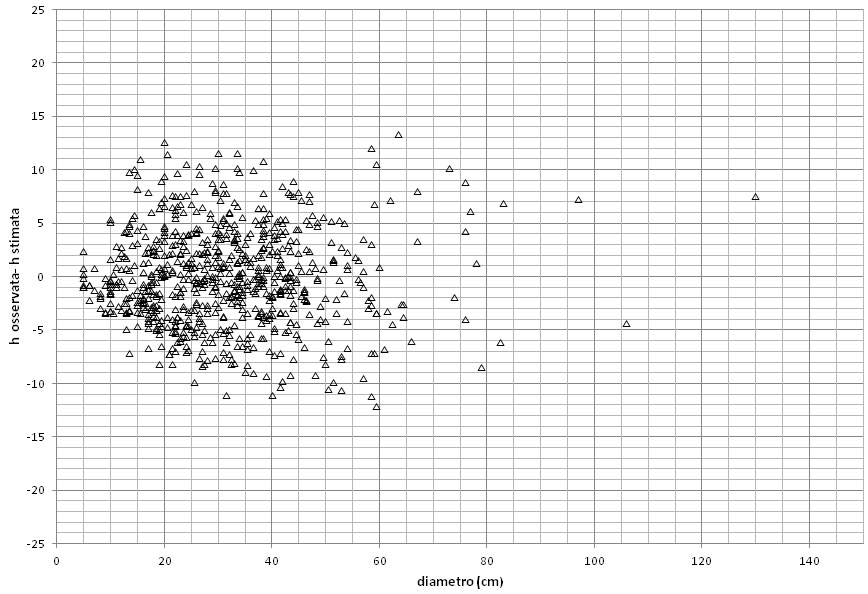
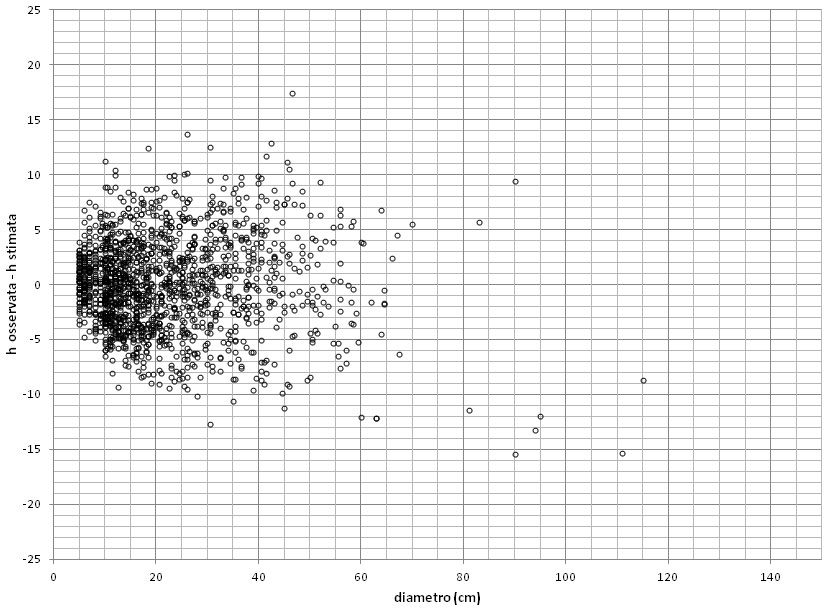
Le Fig. 5 e Fig. 6 (distribuzione dei residui dei modelli di stima) sembrano evidenziare, prevalentemente nel caso delle conifere, fenomeni molto limitati di eteroschedasticità della varianza d’errore di stima all’aumentare della variabile indipendente diametro. La tendenza sembra peraltro limitata alla zona dei diametri piccoli, fino a 20-25 cm. Naturalmente analogo comportamento assumono i residui rispetto all’altro regressore d2. Il fenomeno, che peraltro anche in forme molto più accentuate costituisce quasi la regola in modellistica dendrometrica, non determina particolari conseguenze sulla linearità e correttezza degli stimatori (coefficienti) ma può rendere poco efficienti (consistenti) le stime di intervallo di confidenza degli stessi che, nel caso delle conifere, risulta in pratica leggermente sottostimato.
Fig. 5 - Residui di stima (h osservata - h stimata) della curva guida “media” della relazione h/d (hT5) per il gruppo delle conifere.
Fig. 6 - Residui di stima (h osservata - h stimata) della curva guida “media” della relazione h/d (hT5) per il gruppo delle latifoglie.
La variabilità spiegata dai modelli si attesta in entrambi i casi a livelli appena superiori al 50%. Va ricordato che, a questo stadio, i due modelli base dei grandi gruppi di specie perequano un fenomeno ipsometrico molto ampio sulla sola base della variabile esplicativa diametro e che tale fenomeno è invece influenzato da molte altre variabili non considerate dai soli modelli base (specie, fertilità, stadio cronologico). La presa in considerazione di tali variabili è demandata al sistema tariffario nel suo insieme e cioè non a una ma a nove curve guida della relazione h/d, la cui definizione verrà chiarita nel successivo paragrafo.
Le serie ipsometriche derivate dalla perequazione base
Similmente a quanto si verifica prevalentemente nel caso dei sistemi di Tariffe costruite nell’arco alpino, nel sistema TaCAL si sono adottati indicatori a numero intero (da 1 a 9) delle serie ipsometriche tariffarie, con 1 che identifica la tariffa “migliore” (quota della serie ipsometrica più elevata e volume più alto a parità di diametro) e con 9 la “peggiore”. L’esperienza depone per una maggiore rapidità di assimilazione concettuale e mnemonica da parte degli utenti di tale sistema identificativo che aiuta nel fare le relative interpretazioni e confronti dei sottesi fenomeni ipso/stereometrici.
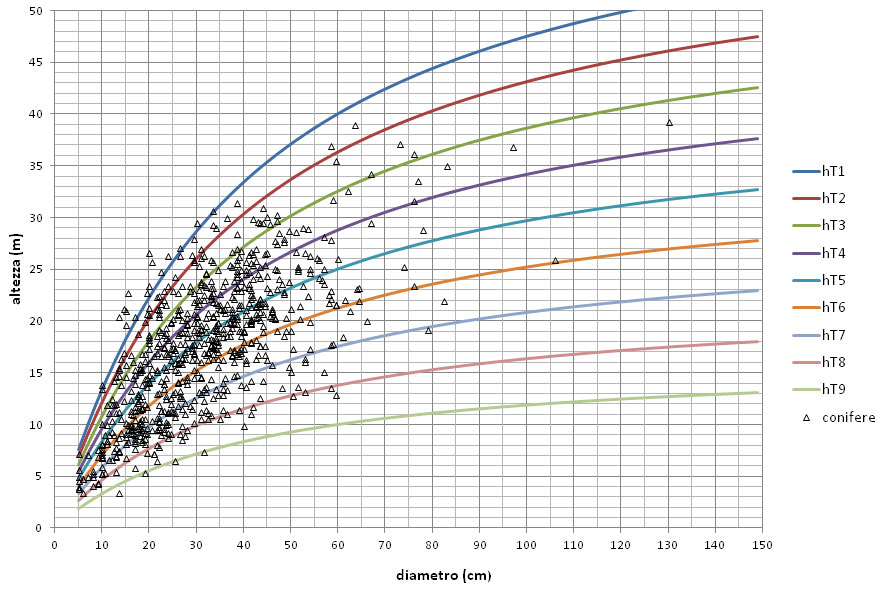
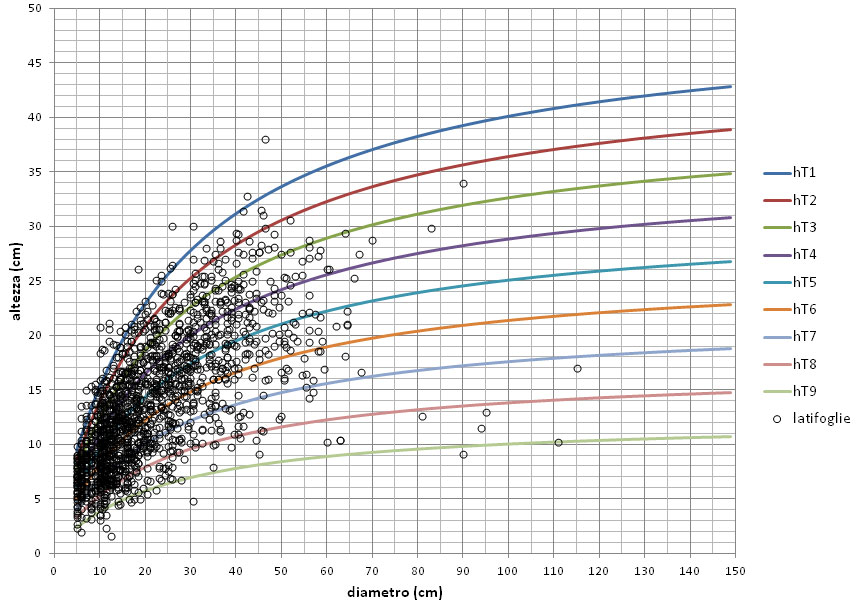
A partire dalla specifica curva guida media della relazione h/d, le 9 curve guida definitive degli inquadramenti ipsometrici delle conifere e, rispettivamente, delle latifoglie, sono state prodotte semplicemente moltiplicando l’altezza fornita dal rispettivo modello base per un coefficiente cn (con n da 1 a 9), variabile da 1.6 a 0.4 (con passo 0.15, in diminuzione), ottenendo l’altezza specifica riferita ad ogni serie ipsometrica considerata. In sostanza, è stato adottato un “passo” di adeguamento ipsometrico in aumento o in diminuzione del 15% dell’altezza della curva guida media. Come si può notare dalle Fig. 7 e Fig. 8, in tal modo i due “ventagli” di 9 serie ipsometriche vanno sostanzialmente a coprire l’intero campo di manifestazione ipsometrica riscontrata negli alberi modello sia nel caso delle conifere che nel caso delle latifoglie. Si tenga presente che i pochi casi di soggetti al di fuori del ventagli sono in gran parte entro la “fascia di rappresentazione” (che si estende anche verso l’alto) della curva ipsometrica della tariffa 1. Qualora in futuro emergessero necessità di migliore rappresentazione dei fenomeni ipsometrici in tale zona si potrebbe facilmente istituire la Tariffa “0”.
Fig. 7 - Andamento delle curve guida standard (dalla 1 alla 9) della relazione h/d per il gruppo di specie delle conifere.
Fig. 8 - Andamento delle curve guida standard (dalla 1 alla 9) della relazione h/d per il gruppo di specie delle latifoglie.
Correlazione dell’indicatore di tariffa tra specie diverse
Un aspetto problematico del sistema ipsometrico TaCAL a sole due facies ipsometriche per conifere e latifoglie, riguarda sicuramente la correlazione nell’indicatore di tariffa tra specie diverse in popolamenti misti, soprattutto laddove specie minoritarie non evidenziano un numero di soggetti sufficiente per l’individuazione della relazione h/d sulla base di rilievo apposito che, va ricordato e sottolineato, rappresenta sempre l’approccio applicativo corretto che pone al riparo da qualsiasi errore di attribuzione. Peraltro in tali casi l’incidenza di una eventuale errata attribuzione di tariffa risulta anche di minore incidenza sulla stima della provvigione globale.
Qualora TaCAL fosse stato basato su 20 “ventagli” ipsometrici di singola specie (sempre a 9 livelli ciascuno), si potrebbe ritenere, almeno in prima approssimazione e sempre che si parli di specie i cui soggetti siano analogamente distribuiti nelle classi sociali (e nelle stesse classi cronologiche in popolamenti coetanei), che una assegnazione dello stesso indicatore di tariffa della specie principale anche alla specie minoritaria apparirebbe legittimo. La circostanza, largamente frequente ad esempio negli inventari assestamentali in Trentino, si basa sulla considerazione che, nella stessa stazione e con i vincoli di cui sopra, specie diverse esprimerebbero ciascuna le stesse capacità relative di esplicazione del fenomeno ipsometrico rispetto alle proprie potenzialità intrinseche, appunto connotabili da uguale indicatore di tariffa. In realtà, tali traslazioni sono sempre problematiche in sé stesse, soprattutto se effettuate a livello di intere particelle e non di popolamenti omogenei per fertilità e classe cronologica, e non infrequentemente portano ad errori con qualche conseguenza sul piano della stima delle masse.
In un sistema ipsometrico a sole due fasce ipsometriche standard come è quello di TaCAL è evidente la presenza di difficoltà nel “traslare” l’indicatore di tariffa tra specie in quanto esse occupano fasce esplicative anche molto diverse nell’ambito del proprio gruppo di 9 andamenti standard e a maggior ragione tra i due grandi gruppi delle conifere e delle latifoglie. Ciò si verifica soprattutto per le specie meno diffuse nei confronti di quelle principali e tra boschi del piano basale e boschi di montagna.
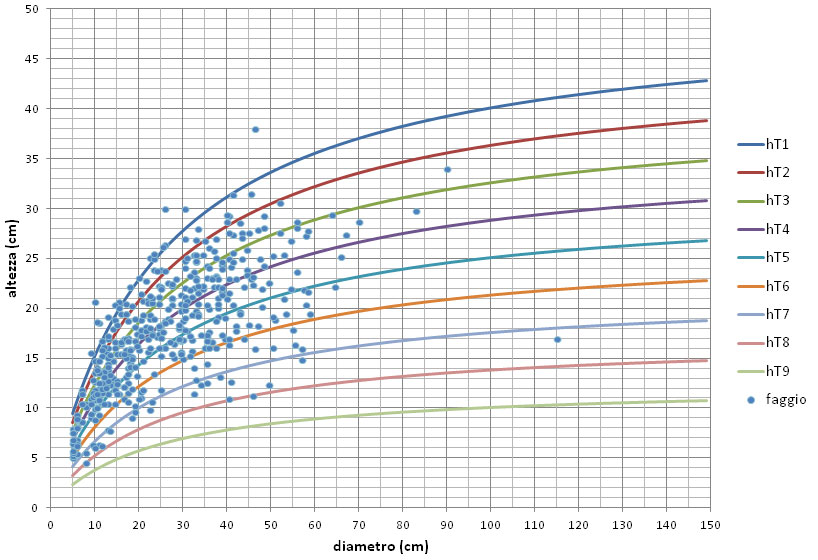
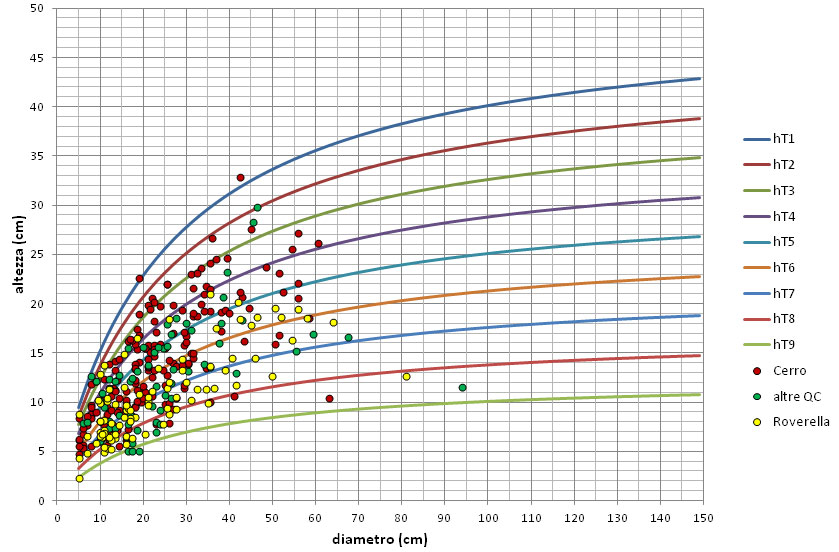
Si notino nelle Fig. 9 e Fig. 10 esempi dell’esplicazione riscontrata per specie diverse nei rispettivi fenomeni ipsometrici. Si può osservare come Faggio da una parte e Querce dall’altra mostrino collocazioni ipsometriche differenziate rispettivamente verso l’alto e verso il basso e come il fenomeno sia accentuato nella Roverella (che ovviamente non è peraltro riscontrabile in consociazione col Faggio).
Fig. 9 - Andamento delle curve guida standard della relazione h/d del gruppo di specie delle Latifoglie e del fenomeno ipsometrico manifestato dagli alberi modello di Faggio rilevati nella campagna INFC.
Fig. 10 - Andamento delle curve guida standard della relazione h/d del gruppo di specie delle latifoglie e del fenomeno ipsometrico manifestato dagli alberi modello di Cerro, altre Querce caducifoglie e Roverella rilevati nella campagna INFC
Per ovviare a tale problema di “attribuzione correlata” dell’indicatore di tariffa a specie consociate minoritarie, per tutte le specie o gruppi specifici sono stati visualizzati separatamente e studiati i campi di esplicazione ipsometrica caratteristica, come desumibili dagli alberi modello INFC utilizzati per la costruzione del sistema di inquadramento ipsometrico TaCAL (Tab. 6). Le citate Fig. 9 e Fig. 10 sono appunto esempio di tale analisi a seguito della quale si è prodotta la Tab. 6.
Tab. 6 - Quadro di correlazione dell’indicatore di tariffa tra specie diverse nel sistema ipsometrico TaCAL.
| Tavola tariffaria TaCal |
Specie o gruppo di specie | Tmax | Tmed | Tmin | Abete bianco | Douglasia | Pino Laricio | Pino d’Aleppo | Pino marittimo | Pino domestico | Pini alloctoni | Cipressi | Faggio | Castagno | Cerro | altre Querce cad. | Roverella | Leccio | Sughera | Aceri | Frassini | Carpini | Ontani | Eucalitti | Robinia | Pioppi | altre lat. maggiori | altre lat. minori |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Abete bianco | Abete bianco | 1 | 4 | 8 | 0 | 0 | 1 | 3 | 2 | 3 | 2 | 3 | 0 | 0 | 1 | 2 | 2 | 2 | 4 | 1 | 3 | 2 | 0 | 1 | 2 | 1 | 2 | 4 |
| Douglasia | Douglasia | 1 | 4 | 6 | 0 | 0 | 1 | 3 | 2 | 3 | 2 | 3 | 0 | 0 | 1 | 2 | 2 | 2 | 4 | 1 | 3 | 2 | 0 | 1 | 2 | 1 | 2 | 4 |
| Pino Laricio | Pino Laricio | 1 | 5 | 9 | -1 | -1 | 0 | 2 | 1 | 2 | 1 | 2 | -1 | -1 | 0 | 1 | 1 | 1 | 3 | 0 | 2 | 1 | -1 | 0 | 1 | 0 | 1 | 3 |
| Pino d’Aleppo | Pino d’Aleppo | 4 | 7 | 9 | -3 | -3 | -2 | 0 | -1 | 0 | -1 | 0 | -3 | -3 | -2 | -1 | -1 | -1 | 1 | -2 | 0 | -1 | -3 | -2 | -1 | -2 | -1 | 1 |
| Pino marittimo | Pino marittimo | 4 | 6 | 8 | -2 | -2 | -1 | 1 | 0 | 1 | 0 | 1 | -2 | -2 | -1 | 0 | 0 | 0 | 2 | -1 | 1 | 0 | -2 | -1 | 0 | -1 | 0 | 2 |
| Pino domestico | Pino domestico | 5 | 7 | 9 | -3 | -3 | -2 | 0 | -1 | 0 | -1 | 0 | -3 | -3 | -2 | -1 | -1 | -1 | 1 | -2 | 0 | -1 | -3 | -2 | -1 | -2 | -1 | 1 |
| Pini alloctoni | Pini alloctoni | 3 | 6 | 8 | -2 | -2 | -1 | 1 | 0 | 1 | 0 | 1 | -2 | -2 | -1 | 0 | 0 | 0 | 2 | -1 | 1 | 0 | -2 | -1 | 0 | -1 | 0 | 2 |
| Cipressi | Cipressi | 5 | 7 | 9 | -3 | -3 | -2 | 0 | -1 | 0 | -1 | 0 | -3 | -3 | -2 | -1 | -1 | -1 | 1 | -2 | 0 | -1 | -3 | -2 | -1 | -2 | -1 | 1 |
| Faggio | Faggio | 1 | 4 | 9 | 0 | 0 | 1 | 3 | 2 | 3 | 2 | 3 | 0 | 0 | 1 | 2 | 2 | 2 | 4 | 1 | 3 | 2 | 0 | 1 | 2 | 1 | 2 | 4 |
| Castagno | Castagno | 1 | 4 | 8 | 0 | 0 | 1 | 3 | 2 | 3 | 2 | 3 | 0 | 0 | 1 | 2 | 2 | 2 | 4 | 1 | 3 | 2 | 0 | 1 | 2 | 1 | 2 | 4 |
| Cerro | Cerro | 1 | 5 | 8 | -1 | -1 | 0 | 2 | 1 | 2 | 1 | 2 | -1 | -1 | 0 | 1 | 1 | 1 | 3 | 0 | 2 | 1 | -1 | 0 | 1 | 0 | 1 | 3 |
| altre Querce cad. | 2 | 6 | 9 | -2 | -2 | -1 | 1 | 0 | 1 | 0 | 1 | -2 | -2 | -1 | 0 | 0 | 0 | 2 | -1 | 1 | 0 | -2 | -1 | 0 | -1 | 0 | 2 | |
| Roverella | Roverella | 3 | 6 | 9 | -2 | -2 | -1 | 1 | 0 | 1 | 0 | 1 | -2 | -2 | -1 | 0 | 0 | 0 | 2 | -1 | 1 | 0 | -2 | -1 | 0 | -1 | 0 | 2 |
| Leccio | Leccio | 3 | 6 | 9 | -2 | -2 | -1 | 1 | 0 | 1 | 0 | 1 | -2 | -2 | -1 | 0 | 0 | 0 | 2 | -1 | 1 | 0 | -2 | -1 | 0 | -1 | 0 | 2 |
| Sughera | 6 | 8 | 9 | -4 | -4 | -3 | -1 | -2 | -1 | -2 | -1 | -4 | -4 | -3 | -2 | -2 | -2 | 0 | -3 | -1 | -2 | -4 | -3 | -2 | -3 | -2 | 0 | |
| Aceri | Aceri | 2 | 5 | 8 | -1 | -1 | 0 | 2 | 1 | 2 | 1 | 2 | -1 | -1 | 0 | 1 | 1 | 1 | 3 | 0 | 2 | 1 | -1 | 0 | 1 | 0 | 1 | 3 |
| Frassini | Frassini | 3 | 7 | 8 | -3 | -3 | -2 | 0 | -1 | 0 | -1 | 0 | -3 | -3 | -2 | -1 | -1 | -1 | 1 | -2 | 0 | -1 | -3 | -2 | -1 | -2 | -1 | 1 |
| Carpini | Carpini | 4 | 6 | 8 | -2 | -2 | -1 | 1 | 0 | 1 | 0 | 1 | -2 | -2 | -1 | 0 | 0 | 0 | 2 | -1 | 1 | 0 | -2 | -1 | 0 | -1 | 0 | 2 |
| Ontani | Ontani | 2 | 4 | 8 | 0 | 0 | 1 | 3 | 2 | 3 | 2 | 3 | 0 | 0 | 1 | 2 | 2 | 2 | 4 | 1 | 3 | 2 | 0 | 1 | 2 | 1 | 2 | 4 |
| Eucalitti | Eucalitti | 2 | 5 | 8 | -1 | -1 | 0 | 2 | 1 | 2 | 1 | 2 | -1 | -1 | 0 | 1 | 1 | 1 | 3 | 0 | 2 | 1 | -1 | 0 | 1 | 0 | 1 | 3 |
| Robinia | Robinia | 5 | 6 | 9 | -2 | -2 | -1 | 1 | 0 | 1 | 0 | 1 | -2 | -2 | -1 | 0 | 0 | 0 | 2 | -1 | 1 | 0 | -2 | -1 | 0 | -1 | 0 | 2 |
| Altre latifoglie | Pioppi | 3 | 5 | 7 | -1 | -1 | 0 | 2 | 1 | 2 | 1 | 2 | -1 | -1 | 0 | 1 | 1 | 1 | 3 | 0 | 2 | 1 | -1 | 0 | 1 | 0 | 1 | 3 |
| altre lat. maggiori | 3 | 6 | 8 | -2 | -2 | -1 | 1 | 0 | 1 | 0 | 1 | -2 | -2 | -1 | 0 | 0 | 0 | 2 | -1 | 1 | 0 | -2 | -1 | 0 | -1 | 0 | 2 | |
| altre lat. minori | 5 | 8 | 9 | -4 | -4 | -3 | -1 | -2 | -1 | -2 | -1 | -4 | -4 | -3 | -2 | -2 | -2 | 0 | -3 | -1 | -2 | -4 | -3 | -2 | -3 | -2 | 0 |
La tabella indica per ogni specie in riga, a sinistra, gli indicatori di tariffa minimo (“migliore”), medio e massimo riscontrati per la specie nella realtà calabrese, mentre a destra i differenziali positivi o negativi da aggiungere (algebricamente) all’indicatore di tariffa determinato per la specie considerata in uno specifico caso per ottenere “in modo correlato” il probabile indicatore di tariffa di altra specie minoritaria (indicata in colonna) eventualmente presente nella stessa stazione.
Si sottolinea che la tabella si può applicare (con attento controllo delle conclusioni) nei casi in cui la/le specie minoritaria/e non siano presenti in numero di soggetti sufficienti per poter determinare tramite rilievi ipsometrici propri l’indicatore di tariffa corretto e sempre che si parli di specie i cui soggetti siano analogamente distribuiti nelle classi sociali (e classe cronologica in popolamenti coetanei). Si può notare che i differenziali sono riportati in tabella relazionando qualsiasi specie con qualsiasi altra: è quanto mai evidente come molte combinazioni teoriche siano di fatto altamente improbabili laddove riguardino specie ecologicamente incompatibili e quindi non riscontrabili in consociazione.
Le serie di volumi e delle fitomasse in funzione del diametro
Dal momento che i sistemi di tariffe si basano su una sottostante funzione stereometrica a doppia entrata [v = ƒ (d, h)] di specie o gruppo di specie, gli andamenti standard della relazione h/d fin qui citati e studiati in sede di sviluppo del sistema di inquadramento ipsometrico TaCAL hanno ovviamente fornito la funzione di determinazione del parametro altezza da inserire nelle funzioni stereometriche a doppia entrata. Come già ricordato, tali funzioni sono quelle sviluppate per l’Inventario forestale nazionale INFC 2005 ([12]).
A seguito di tale operazione per ognuna delle specie (o gruppi) nella quarta colonna della Tab. 6 sono state approntate le rispettive serie di volumi [v = f(d)] corrispondenti ad ognuno dei 9 andamenti ipsometrici del gruppo delle conifere o, rispettivamente, delle latifoglie, a seconda del gruppo di inquadramento ipsometrico al quale ogni specie appartiene. Si ricorda che i modelli INFC 2005 riguardano volumi dendrometrici del fusto e dei rami grossi fino a 5 cm di diametro minimo in entrambi i casi.
Si fa notare che in questa fase si verifica la separazione/caratterizzazione per specie dei modelli [v = f(d)]. Infatti i modelli stereometrici a doppia entrata INFC 2005 hanno diversa configurazione dei coefficienti b1, b2, b3 per le 20 specie di Tab. 6, al di là del fatto che la serie ipsometrica sia identica per tutte le specie di conifere e rispettivamente di latifoglie.
Detti modelli sono del tipo (eqn. 2):
dove v è il volume del soggetto arboreo, d è il diametro dello stesso ad 1.3 m, h è l’altezza totale del soggetto derivante dal modello ipsometrico per lo specifico indicatore di tariffa (da 1 a 9), b1, b2, b3 sono i coefficienti del modello stereometrico a doppia entrata INFC 2005, variabili con la specie cui il soggetto appartiene.
In modo del tutto analogo a quelle dei volumi dendrometrici individuali e ovviamente utilizzando gli opportuni modelli specifici INFC 2005 delle fitomasse ([12]) per lo stesso insieme di specie di Tab. 6, si sono messe a punto la serie tariffarie: (i) della fitomassa del fusto e dei rami grossi (fino a 5 cm - eqn. 3):
(ii) della fitomassa arborea epigea totale (compresa fascina e fogliame - eqn. 4):
dove ps1 e ps2, sono, rispettivamente, le fitomasse citate in precedenza, b1, b2, b3 sono i coefficienti delle specifiche funzioni di fitomassa INFC 2005, diversi da quelli del modello [2] e ulteriormente diversificati tra modello [3] e modello [4], mentre i regressori d e h hanno i significati consueti.
Si sottolinea che tali insiemi di serie tariffarie si riferiscono a fitomasse anidre (totalmente prive di umidità libera) e non sono assimilabili a pesi secchi commerciali (umidità standard 12%) e tanto meno a pesi freschi. La ragione di tale riferimento fisico risiede nel fatto che tale standard è l’unico utile per eventuali quantificazioni connesse alla fissazione forestale di carbonio in peso per il quale è universalmente accettato il coefficiente del 50% rispetto alla fitomassa in condizioni anidre.
Va ricordato che il sistema TaCAL è quindi il primo sistema tariffario esteso non solo ai volumi individuali ma anche ai due tipi di fitomasse utili in sede di valutazioni connesse alla quantificazione del sequestro forestale di carbonio e quindi all’assorbimento di anidride carbonica (coefficiente moltiplicativo standard di 3.67 rispetto al peso in carbonio).
L’insieme delle serie tariffarie ad una entrata da 1 a 9 in forma numerica tabellare (per diametri ad 1.3 m estesi da 7 a 100 cm) per tutte le specie di Tab. 6 e in riferimento a volume, fitomassa del fusto e dei rami grossi e fitomassa arborea epigea totale sono rappresentate nel documento “TaCAL - Tariffe dei volumi legnosi e delle fitomasse delle principali specie forestali della Calabria” (ottobre 2015), curato dagli Autori del presente contributo e allegato al medesimo (Appendice 1). In tale documento sono riportate anche le strutture modellistiche e tutti i valori dei rispettivi coefficienti in riferimento ai modelli ipsometrici, a quelli di volume e a quelli delle fitomasse ormai più volte citate, nonché i grafici degli andamenti dei valori.
Indicazioni pratiche per l’individuazione della tariffa in sede di applicazione
Sul piano operativo, l’utilizzo del sistema TaCal richiede l’assegnazione di una tariffa a ciascuna area forestale dotata di un certo grado di omogeneità. Al riguardo si sottolinea come il tradizionale livello particellare ispirato a criteri fisiografici di compartimentazione sia inadatto a descrivere le diverse declinazioni ipsometriche che assumono in tali casi i popolamenti sub-particellari, rendendo preferibile l’individuazione di unità di popolamento omogenee di estensione relativamente contenuta.
Il tecnico forestale chiamato a produrre stime di volume legnoso e fitomassa potrà evitare di costruire vere e proprie curve ipsometriche di specie o gruppo specifico misurando solo alcune coppie di valori diametro/altezza (separatamente per ciascuna specie principale) e concentrando il rilievo sui soggetti di dimensioni maggiori (piano dominante e codominante) e piuttosto “anonimi”, cioè privi di caratteri eccezionali in un senso o nell’altro, evitando quindi soggetti superdominanti, di cicli colturali precedenti, con evidenti patologie o danni, completamente sottoposti, ecc. Poiché questa procedura non è finalizzata alla realizzazione di una curva ipsometrica, ma alla individuazione di un valore di indicatore tariffario, le esperienze sinora condotte hanno dimostrato che in popolamenti abbastanza omogenei e non troppo estesi (qualche ettaro) 8-10 osservazioni possono essere un numero congruo. Di tali valori misurati si calcoleranno il diametro medio e l’altezza media (entrambi aritmetici) e si adotterà tale coppia di valori per entrare nel sistema ipsometrico tariffario delle relative specie. In popolamenti con due o più specie presenti in misura significativa, sarà opportuno calcolare la tariffa di ciascuna specie con un rilievo ipso-diametrico separato. Qualora invece nel popolamento in esame siano presenti una o più specie sporadiche o nettamente minoritarie, non ricorrendo i presupposti di efficienza per effettuare rilievi specifici, si potrà fare ricorso alla Tab. 6, individuando i differenziali da sommare (algebricamente) all’indicatore di tariffa stimato per la specie principale per ottenere quello/i delle specie minoritarie.
A titolo di esempio, si ponga che il rilevatore si trovi in un popolamento forestale di Faggio con presenza largamente minoritaria di Aceri e altre latifoglie maggiori. Egli procederà alla misurazione di diametro e altezza su un numero sufficiente di soggetti di faggio, scelti con i criteri prima illustrati. Sempre a titolo di esempio, siano i valori medi aritmetici di diametro e altezza di tali soggetti pari rispettivamente a 40 cm e 20.5 m. Tali valori si collocano nella fascia superiore dell’intervallo ipsometrico rappresentato dalla curva guida della tariffa 5 nel sistema di relazione ipso-diametrica per le latifoglie della Calabria (Fig. 8). Assegnata quindi la tariffa 5 al faggio, dalla Tab. 6 il rilevatore verificherà che alla tariffa calcolata per il faggio occorre sommare 1 per desumere la probabile tariffa correlata degli aceri, ottenendo quindi per quest’ultimi la tariffa 6. Dalla Tab. 6 si desume anche che è 2 il valore da sommare all’indicatore del faggio per le altre latifoglie maggiori, ottenendo quindi l’indicatore di tariffa correlato (5+2=) 7 per queste ultime.
Si sottolinea ancora una volta che quest’ultima procedura è ragionevolmente applicabile quando non ricorrano i presupposti per un rilievo ipso-diametrico indipendente di una specie e quando il popolamento presenti una sufficiente omogeneità sul piano stazionale e strutturale.
Conclusioni
Sviluppato nell’ambito del progetto PON “Ambi.Tec.Fil.Legno” (ALForLab), questo studio ha portato a mettere a punto un articolato sistema di serie tariffarie di cubatura, esteso alle fitomasse, valido per tutte le specie forestali principali della Calabria, destinato a delineare le coordinate di espressione dendrometrica degli alberi forestali ai fini dell’inventariazione, sia a scala regionale che assestamentale. La creazione di un contesto univoco e unitario della dendrometria delle foreste calabresi appariva importante innanzitutto per sostenere fondamentali approcci metodologici e applicativi del progetto ALForLab connessi al monitoraggio delle risorse forestali regionali e locali mediante l’impiego di tecnologie avanzate di telerilevamento (LiDAR), ma anche nella previsione di auspicabili processi di uniformazione di metodi e procedure dell’inventariazione assestamentale secondo riferimenti compatibili con gli standard nazionali e suscettibili di un alto grado di informatizzazione nella raccolta, trattamento e diffusione dell’informazione inventariale forestale. Tutto ciò imponeva il superamento della dimensione pur ricca di circa cinquanta tavole locali sviluppate nella storia “dendrometrica” del settore forestale calabro a vario titolo impiegate nella pianificazione, nonché l’arricchimento dell’informazione, superando quella esclusivamente volumetrica per fornire anche quella delle fitomasse, oggi indispensabile nei processi di valutazione della fissazione forestale del carbonio.
Lo studio è indubbiamente ispirato ad un pragmatismo operativo che ha spesso prevalso su approfondimenti modellistici particolarmente sofisticati, tuttavia è basato su un campione di soggetti per gli inquadramenti ipsometrici di particolare ampiezza e rappresentatività territoriale, quello dei rilievi INFC 2005, inusuale in studi di questo tipo.
Ringraziamenti
Il presente studio è stato realizzato nell’ambito del Progetto “ALForLab” (PON03PE_00024_1) cofinanziato dal Programma Operativo Nazionale Ricerca e Competitività (PON R&C) 2007-2013, attraverso il Fondo Europeo di Sviluppo Regionale (FESR) e risorse nazionali [Fondo di Rotazione (FDR) - Piano di Azione e Coesione (PAC) MIUR].
Gli autori sono particolarmente grati al Corpo Forestale dello Stato per aver messo a disposizione dello studio i dati “nativi” dei rilievi inventariali INFC 2005 della Calabria.
References
CrossRef | Google Scholar
Google Scholar
Online | Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
Google Scholar
CrossRef | Google Scholar
Google Scholar